题目内容
6.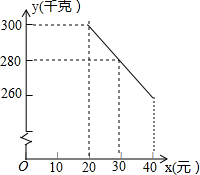 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.(1)求y与x的函数解析式(也称关系式);
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
分析 (1)待定系数法求解可得;
(2)根据:总利润=每千克利润×销售量,列出函数关系式,配方后根据x的取值范围可得W的最大值.
解答 解:(1)设y与x的函数关系式为y=kx+b,
根据题意,得:$\left\{\begin{array}{l}{20k+b=300}\\{30k+b=280}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=340}\end{array}\right.$,
∴y与x的函数解析式为y=-2x+340,(20≤x≤40).
(2)由已知得:W=(x-20)(-2x+340)
=-2x2+380x-6800
=-2(x-95)2+11250,
∵-2<0,
∴当x≤95时,W随x的增大而增大,
∵20≤x≤40,
∴当x=40时,W最大,最大值为-2(40-95)2+11250=5200元.
点评 本题主要考查待定系数法求一次函数解析式与二次函数的应用,根据相等关系列出函数解析式,并由二次函数的性质确定其最值是解题的关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.下列式子是最简二次根式的是( )
| A. | $\sqrt{1.5}$ | B. | $\sqrt{4}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\frac{\sqrt{3}}{3}$ |
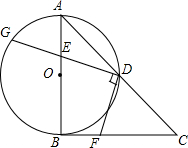 如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.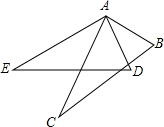 如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是AE=AC(只需添加一个条件即可)
如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是AE=AC(只需添加一个条件即可)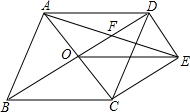 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接AE交OD于点F,连接CE、OE.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接AE交OD于点F,连接CE、OE.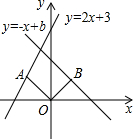 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为2.
如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为2.