题目内容
3.化简:(1)[(3a-2b)2-(a+b)(a-b)-5b2]÷(-$\frac{1}{2}$a)÷16a
(2)$\frac{{x}^{2}-4x+4}{{x}^{2}+x}$÷($\frac{3}{x+1}$-x+1)+$\frac{2}{x+2}$.
分析 (1)原式括号中利用平方差公式及完全平方公式化简,再利用除法法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,再利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:(1)原式=(9a2-12ab+4b2-a2+b2-5b2)÷(-$\frac{1}{2}$a)÷16a
=(8a2-12ab)÷(-$\frac{1}{2}$a)÷16a
=(-16a+24b)÷16a
=-1+$\frac{3b}{2a}$;
(2)原式=$\frac{(x-2)^{2}}{x(x+1)}$÷$\frac{4-{x}^{2}}{x+1}$+$\frac{2}{x+2}$
=$\frac{(x-2)^{2}}{x(x+1)}$×$\frac{x+1}{-(x+2)(x-2)}$+$\frac{2}{x+2}$
=-$\frac{x-2}{x(x+2)}$+$\frac{2}{x+2}$
=$\frac{2-x}{x(x+2)}$+$\frac{2x}{x(x+2)}$
=$\frac{1}{x}$.
点评 本题考查了整式和分式的混合运算,掌握运算的顺序与计算的方法是正确计算的前提.

练习册系列答案
相关题目
14.学校的操场上,升旗的旗杆与地面关系属于( )
| A. | 直线与直线平行 | B. | 直线与平面平行 | C. | 直线与直线垂直 | D. | 直线与平面垂直 |
15.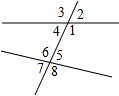 如图,图形中不是同位角的是( )
如图,图形中不是同位角的是( )
 如图,图形中不是同位角的是( )
如图,图形中不是同位角的是( )| A. | ∠3与∠6 | B. | ∠4与∠7 | C. | ∠1与∠5 | D. | ∠2与∠5 |
13. 一次函数y=ax+b的图象如图所示,则化简|a-b|+|b+1|得( )
一次函数y=ax+b的图象如图所示,则化简|a-b|+|b+1|得( )
 一次函数y=ax+b的图象如图所示,则化简|a-b|+|b+1|得( )
一次函数y=ax+b的图象如图所示,则化简|a-b|+|b+1|得( )| A. | 2b-a+1 | B. | 1-a | C. | a-1-2b | D. | a+1 |
 如图,一条公路修到湖边时,经过三次拐弯后,道路恰好与第一次拐弯之前的道路保持平行,如果第一次拐弯的角∠A=120°,第二次拐弯的角∠B=150°,则第三次拐弯的角∠C的度数等于150°.
如图,一条公路修到湖边时,经过三次拐弯后,道路恰好与第一次拐弯之前的道路保持平行,如果第一次拐弯的角∠A=120°,第二次拐弯的角∠B=150°,则第三次拐弯的角∠C的度数等于150°.
 如图,△ABC是等边三角形,P是△ABC的角平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC、BD于点F、Q,若BF=2,则PE的长为$\sqrt{3}$.
如图,△ABC是等边三角形,P是△ABC的角平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC、BD于点F、Q,若BF=2,则PE的长为$\sqrt{3}$.