Question

12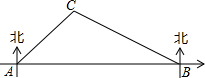．如图，在合肥市轨道交通建设中，规划在A、B两地修建一段地铁，点B在点A的正东方向，由于A、B之间建筑物较多，无法直接测量，现选参照物C，测得C在点A的东北方向上，在点B的北偏西60°方向上，B、C两点间距离为800m．请你求出这段地铁AB的长度．（结果精确到1m，参考数据：$\sqrt{2}$≈1.414，≈1.732）

Answer 1

分析 作CD⊥AB于D，根据正、余弦的概念分别求出BD、CD的长，根据等腰直角三角形的性质求出AD，计算即可．

解答 解：作CD⊥AB于D，
由题意得，∠CAD=45°，∠CBD=30°，
∴BD=BC•cos∠CBD=800×$\frac{\sqrt{3}}{2}$=400$\sqrt{3}$≈693，
CD=$\frac{1}{2}$BC=400，
∴AD=CD=400，
∴AB=AD+BD=1093米．
答：这段地铁AB的长度约为1093米．

点评 本题考查的是解直角三角形的应用-方向角问题，正确标注方向角、熟记锐角三角函数的定义是解题的关键．