题目内容
1.为了宣传普及交通安全常识,学校随机调查了部分学生来校上学的交通方式,并将结果统计后制成如图所示的不完整统计图.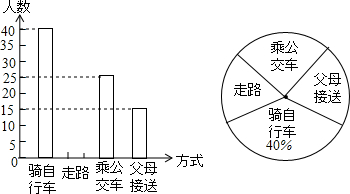
(1)这次被调查学生共有100名,“父母接送”上学的学生在扇形统计图中所占的圆心角为54度;
(2)请把条形图补充完整;
(3)该校有1500名学生,要在“走路”的学生中,选取一名学生代表为交通安全义务宣传员,如果你是一名“走路”同学,那么你被选取的概率是多少?
分析 (1)骑车人数÷骑车所占百分比可得总人数,用父母接送上学占总人数比例乘以360度可得圆心角度数;
(2)用总人数减去其他方式上学的人数可得走路的人数,补充图形即可;
(3)求出全校1500人中走路上学的人,可得概率.
解答 解:(1)40÷40%=100,$\frac{15}{100}$×360°=54°;
(2)走路的人数有:100-40-25-15=20(人),补全图形如下:
(3).∵1500×$\frac{20}{100}$=300,
∴被选取的概率P=$\frac{1}{300}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | $\sqrt{a^2+b^2}$=$\sqrt{a^2}$+$\sqrt{b^2}$ | C. | a2•a3=a5 | D. | $\sqrt{{a}^{4}}$=±a2 |
6.下列计算正确的是( )
| A. | 2(x+y)=2x+y | B. | 2a(a+b)=2a2+b | ||
| C. | 10ab÷(-5a)=-2 | D. | (x-a)(x-b)=x2-(a+b)x+ab |
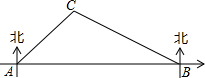 如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732)
如图,在合肥市轨道交通建设中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现选参照物C,测得C在点A的东北方向上,在点B的北偏西60°方向上,B、C两点间距离为800m.请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,≈1.732) 有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.
有一条长40m的篱笆,现借用一堵墙(笔直的、充分长)将篱笆围成一个四边形鸡场.