题目内容
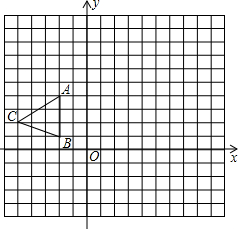 如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)则S△A1B1C1:S△A2B2C2.
考点:作图-位似变换,作图-轴对称变换
专题:
分析:(1)利用关于x轴对称点的性质得出对应点坐标进而得出答案;
(2)利用对应点横坐标与纵坐同时乘以-2,进而得出各点的位置;
(3)利用位似图形的性质得出面积比即可.
(2)利用对应点横坐标与纵坐同时乘以-2,进而得出各点的位置;
(3)利用位似图形的性质得出面积比即可.
解答: 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵△A1B1C1的三个顶点的横坐标与纵坐同时乘以-2,得到对应的点A2,B2,C2,
∴△A1B1C1与△A2B2C2,关于原点位似,位似比为1:2,
∴S△A1B1C1:S△A2B2C2=1:4.
 解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;
(3)∵△A1B1C1的三个顶点的横坐标与纵坐同时乘以-2,得到对应的点A2,B2,C2,
∴△A1B1C1与△A2B2C2,关于原点位似,位似比为1:2,
∴S△A1B1C1:S△A2B2C2=1:4.
点评:此题主要考查了轴对称变换以及位似变换和位似图形的性质,根据题意得出对应点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一元二次方程x2+px-6=0的一个根为2,则p的值为( )
| A、-1 | B、-2 | C、1 | D、2 |
-1
的倒数为( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
方程x2+6x=5的左边配成完全平方后所得方程为( )
| A、(x+3)2=14 |
| B、(x-3)2=14 |
| C、(x+6)2=12 |
| D、以上答案均不对 |
下列图形中,不属于对称图形的是( )
| A、圆 | B、扇形 |
| C、抛物线 | D、直角边长不相等的直角三角形 |
若a-2b-3=0,则(a-2b)2-a+2b-5的值是( )
| A、-5 | B、-11 | C、7 | D、1 |
 如图,点P,C在线段AB上,AC=6cm,PB=10cm,若P是AC的中点,则CB的长是
如图,点P,C在线段AB上,AC=6cm,PB=10cm,若P是AC的中点,则CB的长是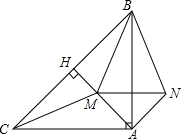 如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.
如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM. 如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°
如图所示,在等腰△ABC中,BC=AC,∠ACB=90°,D、E为斜边AB上的点,且∠DCE=45°