题目内容
10．
如图，C为线段AB上一点，P是线段AC的中点，Q是线段CB的中点，若PQ=2.8cm，则AB=5.6cm．
分析 根据P是线段AC的中点，Q是线段CB的中点，可得CP=AP，CQ=BQ，所以AB=2PQ，据此求出AB的长度是多少即可．
解答 解：∵P是线段AC的中点，Q是线段CB的中点，
∴CP=AP，CQ=BQ，
∴PQ=CP+CQ=AP+BQ=$\frac{1}{2}AB$，
∴AB=2PQ=2×2.8=5.6（cm）．
故答案为：5.6cm．
点评 此题主要考查了两点间的距离的求法，要熟练掌握，解答此题的关键是要判断出：AB=2PQ．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
4．下列因式分解完全正确的是（ ）
| A． | -2a2+4a=-2a（a+2） | B． | -4x2-y2=-（2x+y）2 | ||
| C． | a2-8ab+16b2=（a+4b）2 | D． | 2x2+xy-y2=（2x-y）（x+y） |
5．
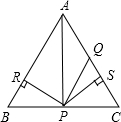如图所示，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论：①AS=AR；②QP∥AR；③△BPR≌△QPS中（ ）
如图所示，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则三个结论：①AS=AR；②QP∥AR；③△BPR≌△QPS中（ ）| A． | 全部正确 | B． | 仅①和③正确 | C． | 仅①正确 | D． | 仅①和②正确 |
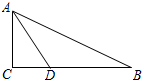已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．