题目内容
20.某校团委为开展“元旦联欢会”,在全校招募主持人,七、八、九年级分别推荐一男一女两位候选主持人.(1)若各年级任选一人,求所选三位主持人恰好同性别的概率;
(2)若九年级的女同学是学校的“金牌主持”,团委只要在其他五人中任选两位同学与之搭档即可,求恰好为“两男一女”的概率.
分析 (1)先画树状图展示所有8种等可能的结果数,再找出三位主持人恰好同性别的结果数,然后根据概率公式求解;
(2)先画树状图展示所有20种等可能的结果数,再找出两男的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为: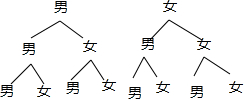
共有8种等可能的结果数,其中三位主持人恰好同性别的结果数为2,
所以所选三位主持人恰好同性别的概率=$\frac{2}{8}$=$\frac{1}{4}$;
(2)画树状图为: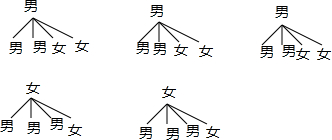
共有20种等可能的结果数,其中两男的结果数为6,
所以恰好为“两男一女”的概率=$\frac{6}{20}$=$\frac{3}{10}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
11.已知点A(1,2),AC⊥x轴于点C,则点C的坐标为( )
| A. | (1,0) | B. | (2,0) | C. | (0,2) | D. | (0,1) |
8.下列运算正确的是( )
| A. | 5ab-3ab=2 | B. | (-a3)2=a6 | C. | a2•a3=a6 | D. | (a-b)2=a2-b2 |
15.设函数f(x)=x(x-1),以下结论正确的是( )
| A. | f(a)+f(-a)=0 | B. | 若f(a)=a,则a=0 | C. | f(a)f($\frac{1}{a}$)=1 | D. | f(a)=f(1-a) |
12.矩形、菱形、正方形都具有的性质是( )
| A. | 对角线相等 | B. | 对角线互相垂直 | C. | 对角线互相平分 | D. | 对角线平分对角 |
 如图,C为线段AB上一点,P是线段AC的中点,Q是线段CB的中点,若PQ=2.8cm,则AB=5.6cm.
如图,C为线段AB上一点,P是线段AC的中点,Q是线段CB的中点,若PQ=2.8cm,则AB=5.6cm.