题目内容
3．
如图，在△ABC中，AB=AD=DC，∠B=60°，则∠C的度数为（ ）| A． | 60° | B． | 30° | C． | 35° | D． | 40° |
分析 先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．
解答 解：∵△ABD中，AB=AD，∠B=60°，
∴∠B=∠ADB=60°，
∴∠ADC=180°-∠ADB=120°，
∵AD=CD，
∴∠C=（180°-∠ADC）÷2=（180°-120°）÷2=30°，
故选：B．
点评 本题考查的是等腰三角形的性质，熟知等腰三角形的两底角相等是解答此题的关键．
练习册系列答案
走进文言文系列答案
相关题目
13．下列实数中是无理数的是（ ）
| A． | 0.38 | B． | $\root{3}{9}$ | C． | $\sqrt{36}$ | D． | -$\frac{22}{7}$ |
18．
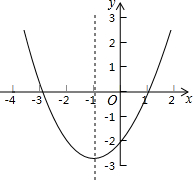已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下说法不正确的是（ ）
已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下说法不正确的是（ ）| A． | 根据图象可得该函数y有最小值 | |
| B． | 当x=-2时，函数y的值小于0 | |
| C． | 根据图象可得a＞0，b＜0 | |
| D． | 当x＜-1时，函数值y随着x的增大而减小 |
如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=2，则EF=4．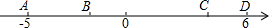
如图，数轴上有A，B，C，D四个整数点（即各点均表示整数），且2AB=BC=3CD．若A，D两点所表示的数分别是-5和6，则线段BD的中点所表示的数是（ ）
13．若点P（m+5，2）与点Q（3，n-5）关于y轴对称，则m，n的值分别是（ ）
| A． | -8，-7 | B． | 8，-7 | C． | -8，7 | D． | 8，7 |