题目内容
8. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=2,则EF=4.
如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=2,则EF=4.
分析 作EG⊥OA于F,根据角平分线的性质得到EG的长度,再根据平行线的性质得到∠OEF=∠COE=15°,然后利用三角形的外角和内角的关系求出∠EFG=30°,利用30°角所对的直角边是斜边的一半解题.
解答 解:作EG⊥OA于G,如图所示:
∵EF∥OB,∠AOE=∠BOE=15°
∴∠OEF=∠COE=15°,EG=CE=2,
∵∠AOE=15°,
∴∠EFG=15°+15°=30°,
∴EF=2EG=4.
故答案为:4.
点评 本题考查了角平分线的性质、平行线的性质、含30°角的直角三角形的性质;熟练掌握角平分线的性质,证出∠EFG=30°是解决问题的关键.

练习册系列答案
相关题目
19.下列式子正确的是( )
| A. | |π-3|=3-π | B. | 若ax=ay,则x=y | C. | a+b>a-b | D. | $-\frac{2}{-9}=\frac{2}{9}$ |
3. 如图,在△ABC中,AB=AD=DC,∠B=60°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠B=60°,则∠C的度数为( )
 如图,在△ABC中,AB=AD=DC,∠B=60°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠B=60°,则∠C的度数为( )| A. | 60° | B. | 30° | C. | 35° | D. | 40° |
13.下列说法正确的是( )
| A. | 多项式2x+3x2+1是二次三项式 | B. | 单项式a的系数是0,次数是0 | ||
| C. | $\frac{xy-1}{2}$是二次单项式 | D. | 单项式-$\frac{2}{5}$x2y的系数是-2,次数是2 |
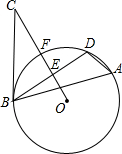 如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.