题目内容
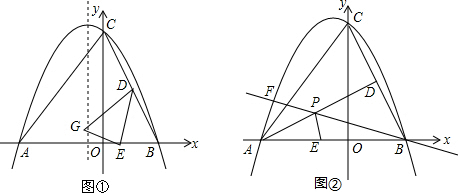
12.已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(-6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点.经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.(1)求抛物线的解析式;
(2)如图①,连接DE,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,连接AD,点F是抛物线上A、C之间的一点,直线BF交AD于点P,连接PE,试探索BP+PE是否存在最小值?若存在,求出这个最小值,并直接写出此时点F的坐标;若不存在,请说明理由.
分析 (1)根据抛物线y=ax2+bx+8经过点A(-6,0),B(4,0),列出a和b的二元一次方程组,求出a和b的值即可;
(2)作DM⊥抛物线的对称轴于点M,设G点的坐标为(-1,n),在Rt△GDM中,利用勾股定理的知识求出n的值,进而求出点G的坐标;
(3)首先求出AC的长,结合题意得到BP+PE=CP+PE,C、P、E应三点共线,要使CP+PE的值最小,则应CE⊥AB,据此解答即可.
解答 解:(1)∵抛物线y=ax2+bx+8经过点A(-6,0),B(4,0),
∴$\left\{\begin{array}{l}{36a-6b+8=0}\\{16a+4b+8=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{2}{3}}\end{array}\right.$,
∴抛物线的解析式是:y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8;
(2)如图①,作DM⊥抛物线的对称轴于点M,
设G点的坐标为(-1,n),
由翻折的性质,可得BD=DG,
∵B(4,0),C(0,8),点D为BC的中点,
∴点D的坐标是(2,4),
∴点M的坐标是(-1,4),DM=2-(-1)=3,
∵B(4,0),C(0,8),
∴BC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴BD=2$\sqrt{5}$,
在Rt△GDM中,
32+(4-n)2=20,
解得n=4±$\sqrt{11}$,
∴G点的坐标为(-1,4+$\sqrt{11}$)或(-1,4-$\sqrt{11}$);
(3)易知OA=6,OB=4,OC=8,
∴AC=$\sqrt{{6}^{2}+{8}^{2}}$=10,AB=10,
∴AC=AB,
∵D是BC的中点,
∴AD⊥BC,则AD是BC的垂直平分线,
∴BP=CP,
∴BP+PE=CP+PE,
∵BP+PE的值要最小,
∴C、P、E应三点共线,要使CP+PE的值最小,则应CE⊥AB,
此时点E与点O重合,
∴CP+PE的最小值应等于OC,
∵OC=8,
即BP+PE的最小值是8,
直线AD的解析式为y=$\frac{1}{2}$x+3,
直线BF的解析式为y=-$\frac{3}{4}$x+3,
联立$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}-\frac{2}{3}x+8}\\{y=-\frac{3}{4}x+3}\end{array}\right.$(x<0),
解得x=-$\frac{15}{4}$,y=$\frac{93}{16}$,
此时F点坐标(-$\frac{15}{4}$,$\frac{93}{16}$).
点评 本题主要考查了二次函数的综合题,此题涉及到待定系数法求二次函数解析式、翻折性质、勾股定理以及三点共线等知识,解答(2)问的关键是求出BD的长,解答(3)问的关键是得到要使CP+PE的值最小,则应CE⊥AB,此题有一定的难度.

| A. | (2m-n)2 | B. | 2 (m-n)2 | C. | 2m-n2 | D. | (m-2n)2 |
 如图,四边形ABCD沿直线AC对折后重合,若AD=3,BC=2,则四边形ABCD周长为10.
如图,四边形ABCD沿直线AC对折后重合,若AD=3,BC=2,则四边形ABCD周长为10.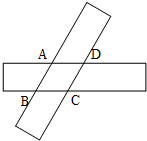 两张长为5宽为1的纸条交叉重叠在一起.
两张长为5宽为1的纸条交叉重叠在一起.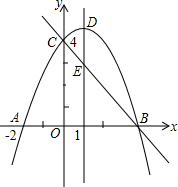 抛物线y=ax2+bx+c(a≠0)与y轴于点C(0,4),与x轴交于点A、B,其中A(-2,0),抛物线对称轴直线x=1与抛物线交于点D,与直线BC交于点E.
抛物线y=ax2+bx+c(a≠0)与y轴于点C(0,4),与x轴交于点A、B,其中A(-2,0),抛物线对称轴直线x=1与抛物线交于点D,与直线BC交于点E.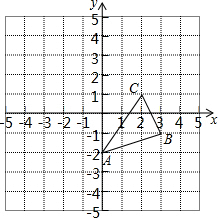 将图中的△ABC作下列变换,画出相应的图形;
将图中的△ABC作下列变换,画出相应的图形; 一次函数y=kx+b图象经过点(0,3)和(4,7).
一次函数y=kx+b图象经过点(0,3)和(4,7). 如图,∠1=100°,∠2=145°,则∠3=65°.
如图,∠1=100°,∠2=145°,则∠3=65°.