题目内容
1. 一次函数y=kx+b图象经过点(0,3)和(4,7).
一次函数y=kx+b图象经过点(0,3)和(4,7).①试求k与b;
②画出这个一次函数图象;
③这个一次函数与x轴交点坐标是(-3,0);
④当x<-3时,y<0;
⑤当x>-3时,y>0;
⑥当0<y<7时,x的取值范围是-3<x<4.
分析 ①利用待定系数法即可求得.
②利用两点法画出函数的图象;
③根据图象求得即可;
④根据图象求得即可;
⑤根据图象和点(3,0,),(4,7)即可求得.
解答 解:①把点(0,3)和(4,7)代入y=kx+b得
$\left\{\begin{array}{l}{b=3}\\{4k+b=7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$;
②函数的图象如图: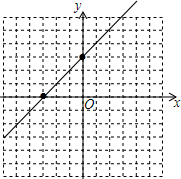
③由图象可知这个函数图象与x轴的交点坐标为(-3,0);
④当x<-3时,y<0;
⑤当x>-3时,y>0;
⑥当0<y<7时,x的取值范围是-3<x<4.
故答案为:(-3,0),<-3,>-3,-3<x<4.,
点评 本题考查了待定系数法求一次函数的解析式,一次函数的图象以及一次函数的性质,熟练掌握一次函数的性质和正确画出函数的图象是解题的关键.

练习册系列答案
相关题目
6.若多项式3x2y2-2xy-x+8y与某多项式的差为x2-2x+1,则这个多项式为( )
| A. | 3x2y2-2xy-x2+8y-3x-1 | B. | 3x2y2-2xy-x2+8y-3x+1 | ||
| C. | 3x2y2-2xy-x2+8y+x+1 | D. | 3x2y2-2xy-x2+8y+x-1 |
 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.