题目内容
关于x的分式方程2k-4+
=
仅有一个实数根,则实数k的取值共有( )
| k+1 |
| x |
| k-5 |
| x+2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:分式方程的解
专题:
分析:先将原方程去分母,两边都乘x(x+2),整理得到(k-2)x2+(2k-1)x+k+1=0.再分两种情况进行讨论:①当k-2≠0时,由于△=(2k-1)2-4(k-2)(k+1)=9>0,得出(k-2)x2+(2k-1)x+k+1=0有两个不相等的实数根.由原方程仅有一个实数根,得出(k-2)x2+(2k-1)x+k+1=0有一个根为0或-2,进而求出k=-1或5;②当k-2=0,即k=2时,方程为3x+3=0,解得x=-1,符合题意.
解答:解:方程两边都乘x(x+2)得,(2k-4)x(x+2)+(k+1)(x+2)=x(k-5),
整理得,(k-2)x2+(2k-1)x+k+1=0.
①当k-2≠0时,∵△=(2k-1)2-4(k-2)(k+1)=9>0,
∴一元二次方程(k-2)x2+(2k-1)x+k+1=0有两个不相等的实数根.
∵关于x的分式方程2k-4+
=
仅有一个实数根,
而x(x+2)=0时,x=0或-2,
∴x=0时,k+1=0,k=-1,此时方程-3x2-3x=0的根为x=0或-1,
其中x=0是原方程的增根,x=-1是原方程的根,符合题意;
x=-2时,4(k-2)-2(2k-1)+k+1=0,k=5,此时方程3x2+9x+6=0的根为x=-2或-1,
其中x=-2是原方程的增根,x=-1是原方程的根,符合题意;
即k=-1或5;
②当k-2=0,即k=2时,方程为3x+3=0,解得x=-1,符合题意;
即k=2.
综上所述,若关于x的分式方程2k-4+
=
仅有一个实数根,则实数k的取值为-1或5或2,共有3个.
故选C.
整理得,(k-2)x2+(2k-1)x+k+1=0.
①当k-2≠0时,∵△=(2k-1)2-4(k-2)(k+1)=9>0,
∴一元二次方程(k-2)x2+(2k-1)x+k+1=0有两个不相等的实数根.
∵关于x的分式方程2k-4+
| k+1 |
| x |
| k-5 |
| x+2 |
而x(x+2)=0时,x=0或-2,
∴x=0时,k+1=0,k=-1,此时方程-3x2-3x=0的根为x=0或-1,
其中x=0是原方程的增根,x=-1是原方程的根,符合题意;
x=-2时,4(k-2)-2(2k-1)+k+1=0,k=5,此时方程3x2+9x+6=0的根为x=-2或-1,
其中x=-2是原方程的增根,x=-1是原方程的根,符合题意;
即k=-1或5;
②当k-2=0,即k=2时,方程为3x+3=0,解得x=-1,符合题意;
即k=2.
综上所述,若关于x的分式方程2k-4+
| k+1 |
| x |
| k-5 |
| x+2 |
故选C.
点评:本题考查了分式方程的解,理解分式方程产生增根的原因是解题的关键.本题有一定难度.

练习册系列答案
相关题目
某商品原售价260元,经过连续两次提价后售价为350元.设平均每次提价的百分率为x,则下列方程中正确的是( )
| A、350(1+x)2=260 |
| B、260(1+x)2=350 |
| C、350(1+2x)=260 |
| D、260(1+2x)=350 |
要使式子-
有意义,字母x的取值必须满足( )
| ||
| x-3 |
A、x≤
| ||
B、x≥-
| ||
C、x≥
| ||
D、x≥
|
某市2014年末,全州普查登记常住人口约为403.25万人.将403.25万用科学记数法表示正确的是( )
| A、4.0325×104 |
| B、4.0325×106 |
| C、4.0325×108 |
| D、4.0325×107 |
 如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )
如图,点D为等边三角形ABC外一点,BD=DA,BE=BA,∠DBE=∠DBC,则∠E的度数是( )| A、10° | B、20° |
| C、30° | D、40° |
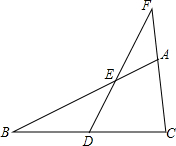 已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF.
已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF. 如图,在△ABC中,AB=AC,D是BC上一点,过点D作DE∥AB,且使DE=AC,连接AD,AE,EC.
如图,在△ABC中,AB=AC,D是BC上一点,过点D作DE∥AB,且使DE=AC,连接AD,AE,EC. 我们定义:如果一个三角形两边的平方和等于第三边平方的5倍,那么这个三角形叫做“理想三角形”.如图,矩形OACB中,O为坐标原点,A在y轴上,B在x轴上,点C的坐标是(2,1),反比例函数y=
我们定义:如果一个三角形两边的平方和等于第三边平方的5倍,那么这个三角形叫做“理想三角形”.如图,矩形OACB中,O为坐标原点,A在y轴上,B在x轴上,点C的坐标是(2,1),反比例函数y=