题目内容
6.化简2m•4n的结果是( )| A. | 2m+2n | B. | (2×4)mn | C. | 2×2mn | D. | (2×4)m+n |
分析 先把原式化为同底数幂的形式,再利用同底数幂的乘法计算即可.
解答 解:2m•4n=2m•22n=2m+2n.
故选A.
点评 此题考查幂的乘方问题,关键是把原式化为同底数幂的形式.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
16.若$\sqrt{(x+2)^{2}}$=x+2,则下列x的取值范围正确的是( )
| A. | x<-2 | B. | x≤-2 | C. | x>-2 | D. | x≥-2 |
14.下列函数,其图象经过点(2,2)的是( )
| A. | y=3x | B. | y=1-2x | C. | y=$\frac{4}{x}$ | D. | y=x2-1 |
11.计算:
(1)$\sqrt{18}$-($\sqrt{3}$+1)0+(-1)2
(2)$\frac{1}{{2+\sqrt{3}}}+\sqrt{27}-6\sqrt{\frac{1}{3}}$.
(1)$\sqrt{18}$-($\sqrt{3}$+1)0+(-1)2
(2)$\frac{1}{{2+\sqrt{3}}}+\sqrt{27}-6\sqrt{\frac{1}{3}}$.
18.若等腰三角形的周长是18,一条边的长是5,则其他两边的长是( )
| A. | 5,8 | B. | 6.5,6.5 | C. | 5,8或6.5,6.5 | D. | 8,6.5 |
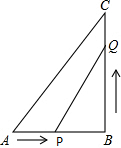 已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.