题目内容
6.(1)如图1,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+$\frac{1}{2}PC$的最小值和PC-$\frac{1}{2}PC$的最大值;(2)如图2,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,那么PD+$\frac{2}{3}PC$的最小值为$\sqrt{106}$,PD-$\frac{2}{3}PC$的最大值为$\sqrt{106}$.
(3)如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,那么PD+$\frac{1}{2}PC$的最小值为$\sqrt{37}$,PD-$\frac{1}{2}PC$的最大值为$\sqrt{37}$.
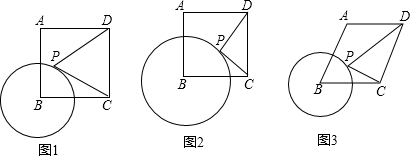
分析 (1)如图1中,在BC上取一点G,使得BG=1.由△PBG∽△CBP,推出$\frac{PG}{PC}$=$\frac{BG}{PB}$=$\frac{1}{2}$,推出PG=$\frac{1}{2}$PC,推出PD+$\frac{1}{2}$PC=DP+PG,由DP+PG≥DG,当D、G、P共线时,PD+$\frac{1}{2}$PC的值最小,最小值为DG=$\sqrt{{4}^{2}+{3}^{2}}$=5.由PD-$\frac{1}{2}$PC=PD-PG≤DG,当点P在DG的延长线上时,PD-$\frac{1}{2}$PC的值最大(如图2中),最大值为DG=5;
(2)如图3中,在BC上取一点G,使得BG=4.解法类似(1);
(3)如图4中,在BC上取一点G,使得BG=4,作DF⊥BC于F.解法类似(1);
解答 解:(1)如图1中,在BC上取一点G,使得BG=1.
∵$\frac{PB}{BG}$=$\frac{2}{1}$=2,$\frac{BC}{PB}$=$\frac{4}{2}$=2,
∴$\frac{PB}{BG}$=$\frac{BC}{PB}$,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴$\frac{PG}{PC}$=$\frac{BG}{PB}$=$\frac{1}{2}$,
∴PG=$\frac{1}{2}$PC,
∴PD+$\frac{1}{2}$PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+$\frac{1}{2}$PC的值最小,最小值为DG=$\sqrt{{4}^{2}+{3}^{2}}$=5.
∵PD-$\frac{1}{2}$PC=PD-PG≤DG,
当点P在DG的延长线上时,PD-$\frac{1}{2}$PC的值最大(如图2中),最大值为DG=5.
(2)如图3中,在BC上取一点G,使得BG=4.
∵$\frac{PB}{BG}$=$\frac{6}{4}$=$\frac{3}{2}$,$\frac{BC}{PB}$=$\frac{9}{6}$=$\frac{3}{2}$,
∴$\frac{PB}{BG}$=$\frac{BC}{PB}$,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴$\frac{PG}{PC}$=$\frac{BG}{PB}$=$\frac{2}{3}$,
∴PG=$\frac{2}{3}$PC,
∴PD+$\frac{2}{3}$PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+$\frac{2}{3}$PC的值最小,最小值为DG=$\sqrt{{5}^{2}+{9}^{2}}$=$\sqrt{106}$.
∵PD-$\frac{2}{3}$PC=PD-PG≤DG,
当点P在DG的延长线上时,PD-$\frac{1}{2}$PC的值最大,最大值为DG=$\sqrt{106}$.
故答案为$\sqrt{106}$,$\sqrt{106}$
(3)如图4中,在BC上取一点G,使得BG=4,作DF⊥BC于F.
∵$\frac{PB}{BG}$=$\frac{2}{1}$=2,$\frac{BC}{PB}$=$\frac{4}{2}$=2,
∴$\frac{PB}{BG}$=$\frac{BC}{PB}$,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴$\frac{PG}{PC}$=$\frac{BG}{PB}$=$\frac{1}{2}$,
∴PG=$\frac{1}{2}$PC,
∴PD+$\frac{1}{2}$PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+$\frac{1}{2}$PC的值最小,最小值为DG,
在Rt△CDF中,∠DCF=60°,CD=4,
∴DF=CD•sin60°=2$\sqrt{3}$,CF=2,
在Rt△GDF中,DG=$\sqrt{(2\sqrt{3})^{2}+(5)^{2}}$=$\sqrt{37}$
∵PD-$\frac{1}{2}$PC=PD-PG≤DG,
当点P在DG的延长线上时,PD-$\frac{1}{2}$PC的值最大(如图2中),最大值为DG=$\sqrt{37}$.
故答案为$\sqrt{37}$,$\sqrt{37}$.
点评 本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识,解题的关键是学会构建相似三角形解决问题,学会用转化的思想思考问题,把问题转化为两点之间线段最短解决,题目比较难,属于中考压轴题.

| A. |  等边三角形 | B. |  正方形 | C. |  平行四边形 | D. |  正五边形 |
| A. | (-a3)2=a6 | B. | xp•yp=(xy)2p | C. | x6÷x3=x2 | D. | (m+n)2=m2+n2 |
| 起步价:3公里以内9元(不再收取燃油附加税) 每公里价格:超过3公里部分,2元/公里(不足1公里按1公里算) 空驶补贴费:超过12公里以上部分,每公里加收公里运价的50% |
(2)有同事告诉他,可以考虑中途到12公里时下车换乘出租车,节省费用,他试了一下,发现换乘车后第二次距离大于3公里,但未超过12公里,而且他还发现比之前不换车总费用少2元,请你算算他的工作单位离家的距离.

| A. | 39π | B. | 29π | C. | 24π | D. | 19π |
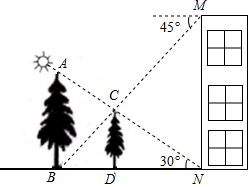 如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)
如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB、CD的高度.(结果保留根号)