题目内容
7.(1)已知xm=3,xn=2,则x3m+2n=108;(2)若x-y=1,则$\frac{1}{2}{x^2}-xy+\frac{1}{2}{y^2}$=$\frac{1}{2}$.
分析 (1)原式利用同底数幂的乘法法则,以及幂的乘方运算法则变形,将已知等式代入计算即可求出值;
(2)原式提取$\frac{1}{2}$,再利用完全平方公式化简,把x-y的值代入计算即可求出值.
解答 解:(1)∵xm=3,xn=2,
∴原式=(xm)3•(xn)2=27×4=108;
(2)∵x-y=1,
∴原式=$\frac{1}{2}$(x2-2xy+y2)=$\frac{1}{2}$(x-y)2=$\frac{1}{2}$.
故答案为:(1)108;(2)$\frac{1}{2}$
点评 此题考查了提公因式与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
2.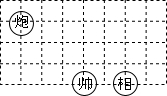 如图所示,这是象棋盘的一部分,若“帅”位于点(-1,-2)上,“相”位于点(1,-2)上,则“炮”位于点( )
如图所示,这是象棋盘的一部分,若“帅”位于点(-1,-2)上,“相”位于点(1,-2)上,则“炮”位于点( )
 如图所示,这是象棋盘的一部分,若“帅”位于点(-1,-2)上,“相”位于点(1,-2)上,则“炮”位于点( )
如图所示,这是象棋盘的一部分,若“帅”位于点(-1,-2)上,“相”位于点(1,-2)上,则“炮”位于点( )| A. | (-3,1) | B. | (-1,2) | C. | (-4,1) | D. | (-4,2) |
17.下列关于分式的判断正确的是( )
| A. | 当x=2时,$\frac{x+1}{x-2}$的值为零 | B. | 无论x为何值,$\frac{3}{x+1}$不可能是整数值 | ||
| C. | 无论x为何值,$\frac{3}{{{x^2}+1}}$的值总为正数 | D. | 当x≠3时,$\frac{x-3}{x}$有意义 |
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为($\frac{1}{2}$π+$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$)cm2.
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为($\frac{1}{2}$π+$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$)cm2. 已知:如图,直线CE和CD相交于点C,AB平分∠EAD,且∠C=∠D,∠EAD=∠C+∠D,求证:AB∥CD.
已知:如图,直线CE和CD相交于点C,AB平分∠EAD,且∠C=∠D,∠EAD=∠C+∠D,求证:AB∥CD.