题目内容
1.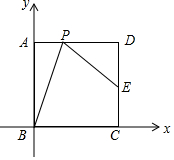 如图,正方形ABCD的边长为2,以点B为原点,BC和AB所在直线分别为x轴和y轴建立平面直角坐标系,点D在第一象限.点E是DC边的中点,P(不与A重合)是AD边上的一动点,设以点P为顶点的抛物线经过点B.
如图,正方形ABCD的边长为2,以点B为原点,BC和AB所在直线分别为x轴和y轴建立平面直角坐标系,点D在第一象限.点E是DC边的中点,P(不与A重合)是AD边上的一动点,设以点P为顶点的抛物线经过点B.(1)当抛物线经过C时,求抛物线的解析式;
(2)在点P的运动过程中,设抛物线与x轴的另一交点为F,BF•AP的值是否发生变化?证明你的结论;
(3)联结PB,PE,在点P运动时,是否存在点P满足PB平分∠APE?若存在,求出P的坐标;若不存在,说明理由.
分析 (1)如图1中,求出点P的坐标,利用待定系数法即可解决问题.
(2)结论:BF•AP的值是变化的.如图2中,作PH⊥BF于H.设P(m,2).由题意可得BF•AP=2m•m=2m2,由此即可判断.
(3)存在.如图3中,作OH⊥PE于H,连接OE.假设OP平分∠APE,由AO⊥AP,OH⊥PE,推出OA=OH=OC,由OE=OE,OP=OP,推出Rt△OEH≌Rt△OEC,Rt△OPA≌Rt△OPH,推出PA=PH,EH=EC=1,设PA=PH=x,在Rt△PDE中,根据PE2=PD2+DE2,可得(x+1)2=(2-x)2+12,解方程即可.
解答 解:(1)如图1中,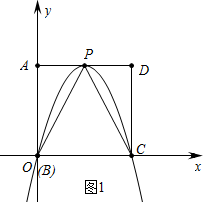
当抛物线经过C时,
∵点P是抛物线的顶点,抛物线经过点B、C,
∴点P在线段BC的垂直平分线上,
∴PB=PC,
在Rt△PBA和Rt△PCD中,
$\left\{\begin{array}{l}{PB=PC}\\{AB=DC}\end{array}\right.$,
∴Rt△PBA≌Rt△PCD,
∴PA=PD=1,
∴P(1,2)
设抛物线的解析式为y=a(x-1)2+2,把(0,0)代入得到a=-2,
∴抛物线的解析式为y=-2(x-1)2+2.
(2)结论:BF•AP的值是变化的.理由如下:
如图2中,作PH⊥BF于H.设P(m,2).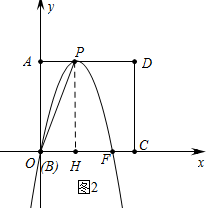
∵∠PAO=∠AOH=∠PHO=90°,
∴四边形APHO是矩形,
∴PA=OH=HF=m,
∴BF=2m,PA=m,
∴BF•AP=2m•m=2m2,
∴BF•AP的值随x的变化而变化.
(3)存在.理由如下,
如图3中,作OH⊥PE于H,连接OE.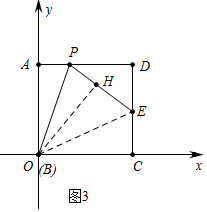
假设OP平分∠APE,∵AO⊥AP,OH⊥PE,
∴OA=OH=OC,∵OE=OE,OP=OP,
∴Rt△OEH≌Rt△OEC,Rt△OPA≌Rt△OPH,
∴PA=PH,EH=EC=1,设PA=PH=x,
在Rt△PDE中,∵PE2=PD2+DE2,
∴(x+1)2=(2-x)2+12,
∴x=$\frac{2}{3}$,
∴p($\frac{2}{3}$,2).
点评 本题考查二次函数综合题、正方形的性质、角平分线的性质定理、勾股定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用勾股定理构建方程,属于中考压轴题.

 如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )
如图,在△ABC中,E、F分别是AD、CE边的中点,且S△BEF=3cm2,则S△ABC为( )| A. | 6 cm2 | B. | 8 cm2 | C. | 10 cm2 | D. | 12 cm2 |
| A. | 9 | B. | 3 | C. | -3 | D. | ±3 |
 如图,半径为5的⊙P与x轴交于点M(4,0),N(10,0),求点P的坐标.
如图,半径为5的⊙P与x轴交于点M(4,0),N(10,0),求点P的坐标.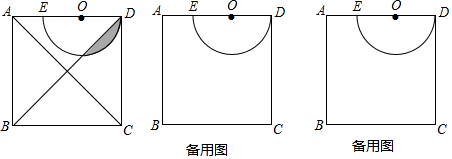
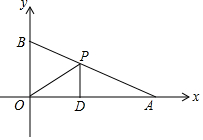 如图,直线y=-$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,点D在x轴上,P是线段AB上的动点,连接DP,OP,过点O作OE平行PD,过点D作DE平行OP得平行四边形OPDE.
如图,直线y=-$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,点D在x轴上,P是线段AB上的动点,连接DP,OP,过点O作OE平行PD,过点D作DE平行OP得平行四边形OPDE.