题目内容
11. 如图,半径为5的⊙P与x轴交于点M(4,0),N(10,0),求点P的坐标.
如图,半径为5的⊙P与x轴交于点M(4,0),N(10,0),求点P的坐标.
分析 直接利用垂径定理结合勾股定理得出PA的长,进而得出答案.
解答  解:过点P作PA⊥MN,于点A,
解:过点P作PA⊥MN,于点A,
∵M(4,0),N(10,0),
∴MN=6,
∵半径为5,PA⊥MN,
∴MA=3,则PA=$\sqrt{{5}^{2}-{3}^{2}}$=4,AO=7,
∴P点坐标为:(7,4).
点评 此题主要考查了垂径定理以及勾股定理,正确得出PA的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.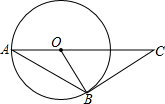 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )
 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠C=40°,则∠ABO的度数是( )| A. | 50° | B. | 40° | C. | 25° | D. | 20度 |
6.把函数y=2x2的图象先沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度得到新函数的图象,则新函数的关系式是( )
| A. | y=2(x+3)2-2 | B. | y=2(x-3)2-2 | C. | y=2(x+3)2+2 | D. | y=2(x-3)2+2 |
16.下面图形是用木条钉成的支架,其中不容易变形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.某商店出售两件衣服,每件卖了200元,其中一件赚了25%,而另一件赔了20%.那么商店在这次交易中( )
| A. | 亏了10元钱 | B. | 赚了10钱 | C. | 赚了20元钱 | D. | 亏了20元钱 |
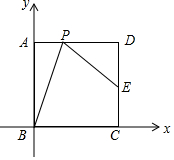 如图,正方形ABCD的边长为2,以点B为原点,BC和AB所在直线分别为x轴和y轴建立平面直角坐标系,点D在第一象限.点E是DC边的中点,P(不与A重合)是AD边上的一动点,设以点P为顶点的抛物线经过点B.
如图,正方形ABCD的边长为2,以点B为原点,BC和AB所在直线分别为x轴和y轴建立平面直角坐标系,点D在第一象限.点E是DC边的中点,P(不与A重合)是AD边上的一动点,设以点P为顶点的抛物线经过点B.