题目内容
15.一次函数y=kx+b的图象过原点和y=2x与x-y=1的交点,那么y=kx+b的解析式是( )| A. | y=2x-1 | B. | y=2x+1 | C. | y=2x | D. | y=x |
分析 联立方程求得y=2x与x-y=1的交点坐标,再利用待定系数法即可求出一次函数的解析式,此题得解.
解答 解:由$\left\{\begin{array}{l}{y=2x}\\{x-y=1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∴y=2x与x-y=1的交点为(-1,-2),
∵一次函数y=kx+b的图象过原点和(-1,-2).
∴$\left\{\begin{array}{l}{-2=-k+b}\\{b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=0}\end{array}\right.$,
∴一次函数的解析式为y=2x.
故选C.
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及待定系数法求一次函数解析式,根据点的坐标利用待定系数法求出一次函数的解析式是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.据网上资料显示,2016年8月止,广西北部湾经济区南北钦防四市总人口约12740000人,其中数据12740000用科学记数法表示为( )
| A. | 1.274×103 | B. | 1.274×104 | C. | 1.274×106 | D. | 1.274×107 |
6.某中学数学兴趣小组12名成员的年龄情况如下表:
则这个小组成员年龄的平均数、中位数和众数分别是( )
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
| A. | 15,16,14 | B. | 13,15,13 | C. | 13,14,14 | D. | 14,14,13 |
3.解分式方程$\frac{2}{x-1}$+$\frac{x+2}{1-x}$=1时,去分母变形后正确的是( )
| A. | 2-(x+2)=1 | B. | 2-x+2=x-1 | C. | 2-(x+2)=x-1 | D. | 2+(x+2)=x-1 |
10.下列说法正确的是( )
| A. | 所有的平行四边形都相似 | B. | 所有的矩形都相似 | ||
| C. | 所有的等边三角形都相似 | D. | 所有的圆内接四边形都相似 |
20.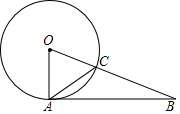 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠BAC=30°,则∠B等于( )| A. | 20° | B. | 30° | C. | 50° | D. | 60° |
7.若关于x的不等式组$\left\{\begin{array}{l}{2x-3<4x+5}\\{x-a>1}\end{array}\right.$的解集是x>-4,则a的取值范围是( )
| A. | a>-4 | B. | a<-5 | C. | a≥-5 | D. | a≤-5 |
4.已知正比例函数y=ax(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)图象的一个交点坐标为(-1,-1),则另一个交点坐标是( )
| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (0,1) |