题目内容
12.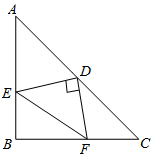 如图,在等腰直角三角形ABC中,∠ABC=90°,AB=2,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,则求四边形BFDE的面积为1.
如图,在等腰直角三角形ABC中,∠ABC=90°,AB=2,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,则求四边形BFDE的面积为1.
分析 连接BD,根据的等腰直角三角形的性质证明△BED≌△CFD,即可推出S△BED=S△DFC,推出S四边形BFDE=S△BDC=$\frac{1}{2}$S△ABC.
解答 解:(1)连接BD.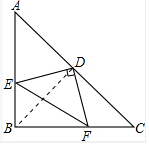
∵D是AC中点,
∴∠ABD=∠CBD=45°,BD=AD=CD,BD⊥AC
∵∠EDB+∠FDB=90°,∠FDB+∠CDF=90°,
∴∠EDB=∠CDF,
在△BED和△CFD中,
$\left\{\begin{array}{l}{∠EBD=∠C}\\{BD=CD}\\{∠EDB=∠CDF}\end{array}\right.$,
∴△BED≌△CFD(ASA),
∴S△BED=S△DFC,
∴S四边形BFDE=S△BDC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×2×2=1.
故答案为1.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了勾股定理的运用,本题中连接BD是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
7.下列计算错误的是( )
| A. | $\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}$=$\frac{x}{y}$ | B. | $\frac{a-1}{b-1}$=$\frac{a}{b}$ | C. | $\frac{a-b}{b-a}$=-1 | D. | $\frac{1}{c}$+$\frac{2}{c}$=$\frac{3}{c}$ |
4.取一次函数y=kx+b部分的自变量x值和对应函数y值如表:
根据信息,下列说法错误的是( )
| x | … | -1 | 0 | 1 | … |
| y | … | -3 | -1 | 1 | … |
| A. | -k+b=-3 | B. | 当x<1时y<1 | ||
| C. | k+b=-1 | D. | 不等式kx+b>-1的解集是x>0 |
2.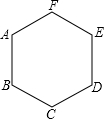 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
 如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )
如图,已知正六边形ABCDEF的边长为5cm,一只电子蚂蚁从顶点A出发沿着正六边形的边爬行,当爬行50cm时,电子蚂蚁离A点的距离为 ( )| A. | $5\sqrt{2}$cm | B. | $5{\sqrt{3}^{\;}}$cm | C. | 5(1+$\sqrt{2}$)cm | D. | 5(1+$\sqrt{3}$)cm |
 如图,在梯形ABCD中,AB∥CD,AD=BC=4,CD=2,AB=6,DM⊥AB,垂足为M,CN⊥AB,垂足为N,点P、Q分别是线段DM、CN上的动点,且DP=NQ,顺次联结AP、PQ、QB,设DP=t.
如图,在梯形ABCD中,AB∥CD,AD=BC=4,CD=2,AB=6,DM⊥AB,垂足为M,CN⊥AB,垂足为N,点P、Q分别是线段DM、CN上的动点,且DP=NQ,顺次联结AP、PQ、QB,设DP=t.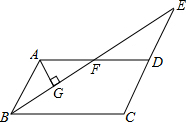 如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点.
如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点. 如图,E是线段AD上一点,AB=AC,BE=CE,求证:
如图,E是线段AD上一点,AB=AC,BE=CE,求证: