题目内容
10.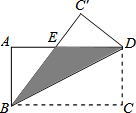 如图,长方形ABCD中,AB=16cm,BC=32cm,如果将该长方形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.
如图,长方形ABCD中,AB=16cm,BC=32cm,如果将该长方形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.| A. | 72 | B. | 90 | C. | 108 | D. | 160 |
分析 易得BE=DE,利用勾股定理求得DE的长,利用三角形的面积公式可得阴影部分的面积.
解答 解:根据翻折的性质可知:∠EBD=∠DBC,
又∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠EBD,
∴BE=DE,
设BE=DE=x,
∴AE=32-x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴AE2+AB2=BE2,
(32-x)2+162=x2,
x=20,
∴S△EDB=$\frac{1}{2}$×20×16=160.
故选:D.
点评 本题考查了折叠的性质:折叠前后的两个图形全等,即对应线段相等,对应角相等.同时也考查了勾股定理,利用勾股定理得到DE的长是解决本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
18.下列命题是真命题的是( )
| A. | 有一个角为60°的三角形是等边三角形 | |
| B. | 底边相等的两个等腰三角形全等 | |
| C. | 有一个角是40°,腰相等的两个等腰三角形全等 | |
| D. | 一边上的中线等于这条边的一半的三角形是直角三角形 |

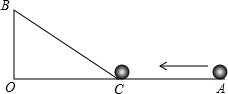 如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少? 如图,在Rt△ABC中,CD是斜边上的中线,CD=3,AC=3.6,求∠DCB的正弦值.
如图,在Rt△ABC中,CD是斜边上的中线,CD=3,AC=3.6,求∠DCB的正弦值.