题目内容
19．
如图，在Rt△ABC中，CD是斜边上的中线，CD=3，AC=3.6，求∠DCB的正弦值．
分析 根据直角三角形的性质，可得AB的长，CD=BD，由等腰三角形的性质得到∠B=∠BCD，然后根据正弦值的定义即可得到结论．
解答 解：∵在Rt△ABC中，CD是斜边上的中线，CD=3，
∴AB=2CD=6，CD=BD，
∴∠B=∠BCD，
∴sin∠DCB=sin∠B=$\frac{AC}{AB}$=$\frac{3.6}{6}$=$\frac{3}{5}$．
点评 本题考查了锐角三角函数的定义，直角三角形的性质、等腰三角形的性质，熟练掌握直角三角形的性质是解题关键．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
9．下列说法正确的是（ ）
| A． | “邻补角相等吗？”是一个命题 | |
| B． | “同位角相等”的逆命题是假命题 | |
| C． | “相等的角是对顶角”是真命题 | |
| D． | “如果两条直线不相交那么一定平行”是真命题 |
10．
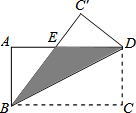如图，长方形ABCD中，AB=16cm，BC=32cm，如果将该长方形沿对角线BD折叠，那么图中阴影部分的面积（ ）cm2．
如图，长方形ABCD中，AB=16cm，BC=32cm，如果将该长方形沿对角线BD折叠，那么图中阴影部分的面积（ ）cm2．| A． | 72 | B． | 90 | C． | 108 | D． | 160 |
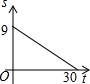由于植被遭遇到严重破坏，某地的土地每年以相同的速度沙化，设t年后该地剩余绿地面积为S万公顷的图象如图所示，则土地沙化的速度为$\frac{3}{10}$万公顷/年，经过30年，该地的土地将全部沙化．
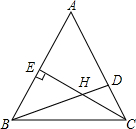△ABC中，∠A：∠ABC：∠ACB=3：4：5，CE是AB上的高，∠BHC=135°，求证：BD⊥AC．