题目内容
7.先化简,再求值:$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x-2}{x-1}$÷$\frac{x-2}{x}$,其中x=-2.分析 根据分式的减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x-2}{x-1}$÷$\frac{x-2}{x}$
=$\frac{{x}^{2}+1}{(x+1)(x-1)}-\frac{x-2}{x-1}•\frac{x}{x-2}$
=$\frac{{x}^{2}+1}{(x+1)(x-1)}-\frac{x}{x-1}$
=$\frac{{x}^{2}+1-x(x+1)}{(x+1)(x-1)}$
=$\frac{1-x}{(x+1)(x-1)}$
=$-\frac{1}{x+1}$,
当x=-2时,原式=$-\frac{1}{-2+1}=1$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列运算正确的是( )
| A. | x3+x4=x7 | B. | 2x3•x2=2x6 | C. | (3x3)2=9x6 | D. | x6÷x3=x2 |
12. 将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )
将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )
 将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )
将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )| A. | 49 | B. | 50 | C. | 52 | D. | 48 |




 如图,由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形,图中以A、B为顶点,面积为4的阵点平行四边形的个数有( )
如图,由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形,图中以A、B为顶点,面积为4的阵点平行四边形的个数有( )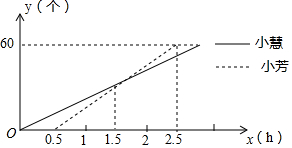 某厂要加工一批新型零件,让小慧和小芳每人试加工60个,小慧一上班就开始试加工,小芳接受半小时培训后再开始试加工,如图所示为小慧和小芳试加工过程中加工的零件数y(个)与加工时间x(h)之间的函数图象,请根据图象所提供的信息解答下列问题:
某厂要加工一批新型零件,让小慧和小芳每人试加工60个,小慧一上班就开始试加工,小芳接受半小时培训后再开始试加工,如图所示为小慧和小芳试加工过程中加工的零件数y(个)与加工时间x(h)之间的函数图象,请根据图象所提供的信息解答下列问题: