题目内容
8. 如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).
分析 根据正方形的性质可找出部分点An的坐标,根据坐标的变化即可找出A8n+1(24n,24n)(n为自然数),再根据2017=252×8+1,即可找出点A2017的坐标.
解答 解:观察,发现:A(0,1)、A1(1,1),A2(2,0),A3(2,-2),A4(0,-4),A5(-4,-4),A6(-8,0),A7(-8,8),A8(0,16),A9(16,16)…,
∴A8n+1(24n,24n)(n为自然数).
∵2017=252×8+1,
∴A2017(2252×4,2252×4),即点A2017的坐标是(21008,21008).
故答案为:(21008,21008).
点评 本题考查了规律型中点的坐标以及正方形的性质,根据点An坐标的变化找出变化规律“A8n+1(24n,24n)(n为自然数)”是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
| x | -1 | 0 | 1 | 3 |
| y | -3 | 1 | 3 | 1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.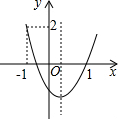 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
①abc<0;
②2a+b>0;
③a+c=1;
④a-b<2.
其中正确结论的有( )
 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:①abc<0;
②2a+b>0;
③a+c=1;
④a-b<2.
其中正确结论的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.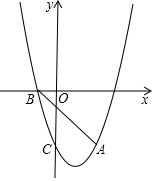 如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.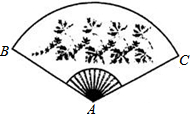 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)