题目内容
2.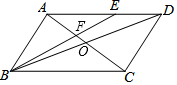 如图,平行四边形ABCD的对角线AC、BD交于点O,E是AD的中点,连接BE交AC于点F,若S△ABF=10,则S△AEF( )
如图,平行四边形ABCD的对角线AC、BD交于点O,E是AD的中点,连接BE交AC于点F,若S△ABF=10,则S△AEF( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据平行四边形的性质得到AD∥BC,AD=BC,求得AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,根据相似三角形的性质得到$\frac{EF}{BF}$=$\frac{AE}{BC}$=$\frac{1}{2}$,于是得到$\frac{{S}_{△AEF}}{{S}_{△ABF}}$=$\frac{1}{2}$,即可得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E是AD的中点,
∴AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵AD∥BC,
∴△AFE∽△CFB,
∴$\frac{EF}{BF}$=$\frac{AE}{BC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△AEF}}{{S}_{△ABF}}$=$\frac{1}{2}$,
∵S△ABF=10,
∴S△AEF=5,
故选D.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若关于y的不等式组$\left\{\begin{array}{l}{\frac{y-1}{2}≥2k}\\{y-k≤4k+6}\end{array}\right.$有解,且关于x的分式方程$\frac{kx}{x-2}$=2+$\frac{3x+2}{2-x}$有非负整数解,则符合条件的所有整数k的和为( )
| A. | -5 | B. | -9 | C. | -12 | D. | -16 |
17.下列说法中,错误的是( )
| A. | 不等式x<5的整数解有无数多个 | B. | 不等式-2x<8的解集是x<-4 | ||
| C. | 不等式x>-5的负整数解是有限个 | D. | -40是不等式2x<-8的一个解 |
 有一块三角形土地,孪爷爷准备将这块土地分成面积相等的四块给他的四个儿子耕种,请你帮他制定出两种划分方案供他选择(画图说明).
有一块三角形土地,孪爷爷准备将这块土地分成面积相等的四块给他的四个儿子耕种,请你帮他制定出两种划分方案供他选择(画图说明).