题目内容
10. 如图,将正方形纸片对折,折痕为EF,展开后继续折叠,使点A落在EF上,折痕为GB,则∠AGB的度数为75°.
如图,将正方形纸片对折,折痕为EF,展开后继续折叠,使点A落在EF上,折痕为GB,则∠AGB的度数为75°.
分析 根据翻折变换的性质表示出BF、AB的长,得出∠BAF,求得∠ABF,进一步得出∠ABG,最后求得∠AGB的度数.
解答 解:∵将正方形纸片对折,折痕为EF,
∴BF=$\frac{1}{2}$AB,∠GAB=90°,
∴∠BAF=30°,
∴ABF=60°,
∵展开后继续折叠,使点A落在EF上,折痕为GB,
∴∠ABG=$\frac{1}{2}$×(90°-60°)=15°,
∴∠AGB=90°-15°=75°.
故答案为:75°.
点评 此题考查折叠的性质,直角三角形的性质:当一条直角边为斜边的一半时,这条直角边所对的角是30°,注意观察折叠前后图形的对应关系.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
1.数轴上的点A表示-2,将点A向左平移5个单位后,再向右平移3个单位到点B,那么,点B表示的数是( )
| A. | 0 | B. | 6 | C. | -10 | D. | -4 |
18.设有一次函数y=kx+3,当x=-1时,y>1;当x=4时,y>-1,则k的取值范围是( )
| A. | -1<k<2 | B. | -1<k<1 | C. | 1<k<2 | D. | 1<k<3 |
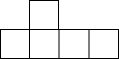 张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.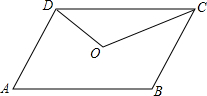 如图,O是?ABCD的对称中心,这个图形是不是中心对称图形?如果认为是,请说明理由;如果认为不是,在原图上添加一些线,使它成为中心对称图形.
如图,O是?ABCD的对称中心,这个图形是不是中心对称图形?如果认为是,请说明理由;如果认为不是,在原图上添加一些线,使它成为中心对称图形.