题目内容
6．
如图，等边△ABC的面积为18，被一平行于BC的矩形所截，且AB被截成三等分，则图中阴影部分的面积是6．
分析 根据相似三角形的面积比等于相似比平方，可求出△AEH及△AFG的面积，根据S阴影=S△AFG-S△AEH，可求出阴影部分的面积．
解答 解：∵EH∥FG∥BC，
∴△AEH∽△AFG∽△ABC，
又∵AB被截成三等份，
∴$\frac{{S}_{△AEH}}{{S}_{△ABC}}$=（$\frac{AE}{AB}$）2=$\frac{1}{9}$，$\frac{{S}_{△AFG}}{{S}_{△ABC}}$=（$\frac{AF}{AB}$）2=$\frac{4}{9}$，
∴S△AEH=2，S△AFG=8，
则S阴影=S△AFG-S△AEH=6．
故答案为：6．
点评 本题考查了相似三角形的判定与性质，解答本题关键是掌握：相似三角形的面积比等于相似比平方，难度一般．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
14．下列计算正确的是（ ）
| A． | 2m+3n=5mn | B． | m2•m3=m6 | C． | m8÷m6=m2 | D． | （-m）3=m3 |
如图，某企业急需汽车，但因资金问题无力购买，想租一辆汽车．一国有公司的条件是每百千米租费110元；一个体公司的条件是每月付工资1000元，油钱600元，另外每百千米付10元，如公司每月有30百千米左右的业务，你建议租个体公司的车．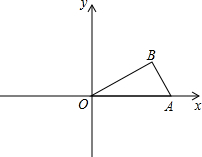
如图，已知放置于平面直角坐标系中的三角板AOB，∠AOB=30°，∠B=90°，AB=1，将△AOB绕O点顺时针旋转30°得到△A1OB1，将△A1OB1绕O点顺时针旋转30°得到△A2OB2，将△A2OB2绕O点顺时针旋转30°得到△A3OB3，依此类推，则B2013的坐标为（$\frac{\sqrt{3}}{2}$，-$\frac{3}{2}$）．
如图所示，有一块长方形土地ABCD，分别被甲、乙两人承包，一条公路GEFH穿过这块地，为发展经济，决定将这条公路尽量修直，为不影响甲、乙两家土地面积，请你设计一种方案来解决这个问题．