题目内容
 如图,△ABC中D为边BC上任意一点,DE,DF分别是△ADB和△ADC的角平分线,连接EF.试判断△DEF的形状,并说明理由.
如图,△ABC中D为边BC上任意一点,DE,DF分别是△ADB和△ADC的角平分线,连接EF.试判断△DEF的形状,并说明理由.考点:三角形内角和定理
专题:
分析:根据角平分线的定义可得∠ADE=∠BDE,∠ADF=∠CDF,然后求出∠EDF=90°,再根据直角三角形的定义解答.
解答:解:∵DE,DF分别是△ADB和△ADC的角平分线,
∴∠ADE=∠BDE,∠ADF=∠CDF,
∴∠EDF=∠ADE+∠ADF=
×180°=90°,
∴△DEF是直角三角形.
∴∠ADE=∠BDE,∠ADF=∠CDF,
∴∠EDF=∠ADE+∠ADF=
| 1 |
| 2 |
∴△DEF是直角三角形.
点评:本题考查了三角形的内角和定理,角平分线的定义,熟记概念并求出∠EDF=90°是解题的关键.

练习册系列答案
相关题目
在一个钝角三角形中,如果一个三角形各边的长度都扩大3倍,那么这个三角形的两个锐角的余弦值( )
| A、都没有变化 |
| B、都扩大3倍 |
| C、都缩小为原来的3倍 |
| D、不能确定是否发生变化 |
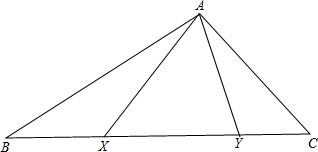 如图,自△ABC的顶点A引两条射线交BC于X,Y,使得∠BAX=∠CAY,求证:
如图,自△ABC的顶点A引两条射线交BC于X,Y,使得∠BAX=∠CAY,求证: 过原点的直线与反比例函数y=
过原点的直线与反比例函数y=