题目内容

19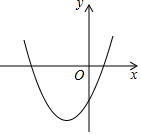．已知二次函数y=ax2+bx+c（a≠0）的图象，关于x的方程ax2+bx+c=0的根的情况是（　　）
A．无实根B．有两相等的实根
C．有两不相等且同号的实根D．有两不等且异号的实根

分析 函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点（原点两侧），即可得出结果．

解答 解：∵函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点，且交点分别在原点两侧，
∴方程ax2+bx+c=0（a≠0）有两不等且异号的实根．
故选：D．

点评 本题考查了抛物线与x轴的交点、一元二次方程根的情况；熟记抛物线与x轴的交点个数和一元二次方程根的关系是解决问题的关键．

练习册系列答案
相关题目
11．若点A（2，m）在抛物线y=x2上，则点A关于原点对称点的坐标是（-2，-4）．
12．函数y=ax2-（3a+1）x+2a+1（a为常数）的图象与坐标轴只有两个交点，则a=0或-$\frac{1}{2}$或-1．
9．一个底面直径是40cm，母线长为60cm的圆锥的侧面展开图的圆心角的度数为120°．
14．若点M，N分别在y=3x和y=4x的图象上，其横坐标分别为m，n，直线MN的函数关系式为y=-3x+b，则$\frac{m}{n}$的值为1．
4．抛物线y=2（x-4）2+1的顶点坐标为（4，1）．
10．有一块木板，如图，请你把它切成三块，然后拼成一个正方形的桌面．请在图中画出剪切线，并把拼成的正方形在图中画出（保留剪切的痕迹，不写画法）
7．已知函数y=k（x+1）（x-$\frac{3}{k}$），下列说法：①方程k（x+1）（x-$\frac{3}{k}$）=-3必有实数根；②若移动函数图象使其经过原点，则只能将图象向右移动1个单位；③当k＞3时，抛物线顶点在第三象限；④若k＜0，则当x＜-1时，y随着x的增大而增大．其中正确的序号是（　　）
A．①②B．．②③C．．①③D．．①③④
8．$\sqrt{36}$的算术平方根是（　　）
A．6B．-6C．±6D．$\sqrt{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网