题目内容
12.函数y=ax2-(3a+1)x+2a+1(a为常数)的图象与坐标轴只有两个交点,则a=0或-$\frac{1}{2}$或-1.分析 当a=0时,可知满足条件,当a≠0时,分当函数图象过原点时和不过原点,当过原点时,可知满足条件,当不过原点时,可知二次函数图象与x轴只有一个交点,令y=0,得到一个关于x的一元二次方程,可知该方程有两个相等的实数根,由一元二次方程根的判别式等于0可求得a的值.
解答 解:当a=0时,函数为y=-x+1,与坐标轴只有两个交点,满足条件;
当a≠0时,分两种情况:
①当函数图象过原点时,则有2a+1=0,解得a=-$\frac{1}{2}$,此时满足条件;
②当函数图象不过原点时,令y=0可得ax2-(3a+1)x+2a+1=0,因其与y轴有一个个交点,所以该方程有两个相等的实数根,
∴△=0,即(3a+1)2-4a(2a+1)=0,整理可得a2+2a+1=0,解得a=-1,
综上可知a的值为0或-$\frac{1}{2}$或-1.
故答案为:0或-$\frac{1}{2}$或-1.
点评 本题主要考查函数与坐标轴的交点,由条件得出函数图象与x轴只有一个交点是解题的关键,注意分类讨论思想的应用.

练习册系列答案
相关题目
20.方程y2+y+2=0的根的情况为( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
7.下列四个平面图形中,不能折叠成无盖的长方体盒子的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
19.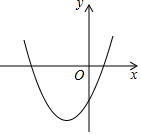 已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )
已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )
已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )| A. | 无实根 | B. | 有两相等的实根 | ||
| C. | 有两不相等且同号的实根 | D. | 有两不等且异号的实根 |
19.点P1(0,y1),P2(2,y2),P3(3,y3)均在二次函数y=-(x-1)2+c的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y3>y1=y2 | C. | y1>y2>y3 | D. | y1=y2>y3 |
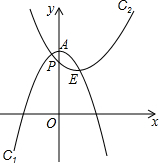 如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).
如图,点A、点E的坐标分别为 (0,3)与(1,2),以点A为顶点的抛物线记为C1:y1=-x2+n;以E为顶点的抛物线记为C2:y2=ax2+bx+c,且抛物线C2与y轴交于点P(0,$\frac{5}{2}$).