题目内容
7.已知函数y=k(x+1)(x-$\frac{3}{k}$),下列说法:①方程k(x+1)(x-$\frac{3}{k}$)=-3必有实数根;②若移动函数图象使其经过原点,则只能将图象向右移动1个单位;③当k>3时,抛物线顶点在第三象限;④若k<0,则当x<-1时,y随着x的增大而增大.其中正确的序号是( )| A. | ①② | B. | .②③ | C. | .①③ | D. | .①③④ |
分析 把函数解析式化为一般式,再结合方程、函数图象等进行判断即可.
解答 解:
∵y=k(x+1)(x-$\frac{3}{k}$)=kx2+(k-3)x-3,
∴方程k(x+1)(x-$\frac{3}{k}$)=-3可化为kx2+(k-3)x-3=-3,即kx2+(k-3)x=0,该方程有实数根,故①正确;
当函数图象向上平移3个单位时,解析式为y=kx2+(k-3)x,则其图象过原点,故②不正确;
在y=kx2+(k-3)x-3中,令x=3可得y=-3,
当k>3时,其对称轴为x=-$\frac{k-3}{2k}$<0,此时其顶点坐标在第三象限,故③正确;
当k<0时,抛物线开口向下,且对称轴在y轴的左侧,但无法确定其在x=-1的左侧还是右侧,故④不正确;
综上可知正确的是①③,
故选C.
点评 本题主要考查二次函数的性质,掌握二次函数与方程、图象的平移等知识是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
20.方程y2+y+2=0的根的情况为( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
19.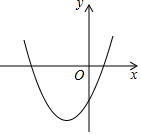 已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )
已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )
已知二次函数y=ax2+bx+c(a≠0)的图象,关于x的方程ax2+bx+c=0的根的情况是( )| A. | 无实根 | B. | 有两相等的实根 | ||
| C. | 有两不相等且同号的实根 | D. | 有两不等且异号的实根 |
2.如图是用相同长度的小棒摆成的一组有规律的图案,图案(1)需要4根小棒,图案(2)需要10根小棒…,按此规律摆下去,第n个图案需要小棒( )根小棒.


| A. | 4n+6 | B. | 6n-2 | C. | 4+6n | D. | 6n |
19.点P1(0,y1),P2(2,y2),P3(3,y3)均在二次函数y=-(x-1)2+c的图象上,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y3>y1=y2 | C. | y1>y2>y3 | D. | y1=y2>y3 |
16.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,x的值应是( )


| A. | 210 | B. | 212 | C. | 268 | D. | 278 |