题目内容
13.如图,在△ABC中,AB=AC,∠B=30°,点D从点B出发,沿B→C方向运动到C(D不与B、C重合),连接AD,作∠ADE=30°,DE交线段AC于E.(1)在点D的运动过程中,若∠BDA=100°,求∠DEC的大小;
(2)在点D的运动过程中,若AB=DC,请证明△ABD≌△DCE;
(3)若BC=6cm,点D的运动速度是1cm/s,运动时间为t(s).在点D的运动过程中,是否存在这样的t,使得△ADE的形状是直角三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由.
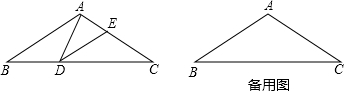
分析 (1)根据等腰三角形的性质得到∠C=∠B=30°,根据已知条件得到∠EDC=180°-100°-30°=50°,于是得到∠DEC=180°-50°-30°=100°;
(2)根据三角形的内角和和平角的定义得到∠CED=∠ADB根据全等三角形的判定定理即可得到结论;
(3)根据三角形的内角和得到∠BAC=120°,求得BD=t,CD=6-t,①如图1,当∠DAE=90,则∠BAD=30°,根据直角三角形的性质列方程求得t的值;②如图2,当∠AED=90°时,则∠DAE=60°,根据等腰三角形的性质列方程求得t的值.
解答 解:(1)∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∵∠BDA=100°,∠ADE=30°,
∴∠EDC=180°-100°-30°=50°,
∴∠DEC=180°-50°-30°=100°;
(2)∵∠C=30°,
∴∠CED+∠CDE=150°,
∵∠ADE=30°,
∴∠ADB+∠CDE=150°,
∴∠CED=∠ADB,
在△ABD和△DCE中,$\left\{\begin{array}{l}{∠ADB=∠DEC}\\{∠B=∠C}\\{AB=DC}\end{array}\right.$,
∴△ABD≌△DCE(AAS);
(3)存在,∵AB=AC,∠B=30°,
∴∠BAC=120°,
∵BC=6cm,点D的运动速度是1cm/s,运动时间为t(s),
∴BD=t,CD=6-t,
①如图1,当∠DAE=90,则∠BAD=30°,
∴∠BAD=∠B=30°,
∴AD=BD=t,
∵∠C=30°,
∴CD=2AD,即6-t=2t,
∴t=2;
②如图2,当∠AED=90°时,则∠DAE=60°,
∴AD平分∠BAC,
∴BD=CD,
即t=6-t,
∴t=3,
综上所述,当t=2或3时,△ADE的形状是直角三角形.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,直角三角形的性质,三角形的内角和,正确的作出图形是解题的关键.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案| A. | a>b | B. | a≥b | C. | a<b | D. | a≤b |
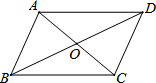 如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使?ABCD成为正方形,下列四种选法错误的是( )
如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使?ABCD成为正方形,下列四种选法错误的是( )


