题目内容
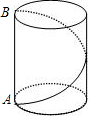
有一圆柱形油罐如图所示,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面半径是 m,高AB为5m,问所建的梯子最短需多少米?
m,高AB为5m,问所建的梯子最短需多少米?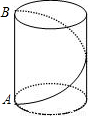
【答案】分析:将圆柱展开,得到矩形,求出矩形对角线即为所建的梯子最短距离.
解答: 解:如图,∵油罐的底面半径是
解:如图,∵油罐的底面半径是 m,
m,
∴油罐的底面周长为2π =12m.
=12m.
又∵高AB为5m,即展开图中,BC=5m,
∴AB= =13m.
=13m.
故所建梯子最短为13m.
点评:此题考查了平面展开--最短路径问题,关键是将圆柱展开为矩形,根据“两点之间线段最短”求出对角线长即可.
解答:
 解:如图,∵油罐的底面半径是
解:如图,∵油罐的底面半径是 m,
m,∴油罐的底面周长为2π
 =12m.
=12m.又∵高AB为5m,即展开图中,BC=5m,
∴AB=
 =13m.
=13m.故所建梯子最短为13m.
点评:此题考查了平面展开--最短路径问题,关键是将圆柱展开为矩形,根据“两点之间线段最短”求出对角线长即可.

练习册系列答案
相关题目
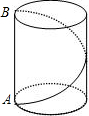 有一圆柱形油罐如图所示,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面半径是
有一圆柱形油罐如图所示,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面半径是 如图所示,有一圆柱形油罐,要从A点环绕油罐搭梯子,正好到A点的正上方B点.梯子最短需要多少米?(已知油罐底面的周长是12m,高AB是5m)
如图所示,有一圆柱形油罐,要从A点环绕油罐搭梯子,正好到A点的正上方B点.梯子最短需要多少米?(已知油罐底面的周长是12m,高AB是5m) 有一圆柱形油罐如图所示,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面半径是
有一圆柱形油罐如图所示,要以A点环绕油罐建梯子,正好到A点的正上方B点,已知油罐的底面半径是 m,高AB为5m,问所建的梯子最短需多少米?
m,高AB为5m,问所建的梯子最短需多少米?