题目内容
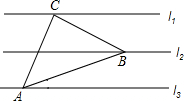 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离均为1,若等腰直角
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离均为1,若等腰直角△ABC的三个项点分别在这三条平行直线上,∠C=90°,求△ABC的面积.
考点:全等三角形的判定与性质,平行线之间的距离,等腰直角三角形
专题:
分析:过A作AD⊥l1交于点D,过B作EF⊥l1交于点E,则可证得△ADC≌△CEB,从而可得CE=AD=2,CD=BE=1,可求得AC的长,进一步可求得△ABC的面积.
解答: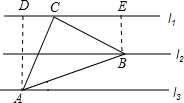 解:如图,过A作AD⊥l1交于点D,过B作EF⊥l1交于点E,
解:如图,过A作AD⊥l1交于点D,过B作EF⊥l1交于点E,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,且∠ACD+∠DAC=90°,
∴∠DAC=∠BCE,
又△ABC为等腰三角形,
∴AC=BC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴CE=AD=2,且BE=1,
在Rt△BCE中,CE=2,BE=1,由勾股定理可求得BC=
=AC,
∴S△ABC=
AC•BC=
×
×
=
.
 解:如图,过A作AD⊥l1交于点D,过B作EF⊥l1交于点E,
解:如图,过A作AD⊥l1交于点D,过B作EF⊥l1交于点E,∵∠ACB=90°,
∴∠ACD+∠BCE=90°,且∠ACD+∠DAC=90°,
∴∠DAC=∠BCE,
又△ABC为等腰三角形,
∴AC=BC,
在△ADC和△CEB中,
|
∴△ADC≌△CEB(AAS),
∴CE=AD=2,且BE=1,
在Rt△BCE中,CE=2,BE=1,由勾股定理可求得BC=
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
点评:本题主要考查全等三角形的判定和性质,利用三角形全等求得CE=2从而求出BC的长是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 如图,四边形ABCD中,∠ADB=∠ABC=105°,∠DBC=75°,AB=DC=15,则S△BCD为
如图,四边形ABCD中,∠ADB=∠ABC=105°,∠DBC=75°,AB=DC=15,则S△BCD为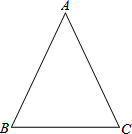 如图,△ABC中,AB=AC=4
如图,△ABC中,AB=AC=4
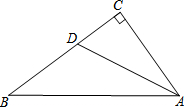 如图,∠C=90°,∠BAD=∠CAD,若BC=11cm,BD=7cm,则点D到AB的距离为
如图,∠C=90°,∠BAD=∠CAD,若BC=11cm,BD=7cm,则点D到AB的距离为