题目内容
已知一个扇形的面积是100m2,现将它的圆心角扩大为原来的2倍,而将它的半径缩小为原来的
,这样所得的扇形面积是多少?
| 1 |
| 2 |
考点:扇形面积的计算
专题:
分析:设原来扇形的圆心角为α,半径为λ,则后来扇形的圆心角为2α,半径为
λ;求出
=100,进而求出
=
×
=50,问题即可解决.
| 1 |
| 2 |
| απλ2 |
| 360 |
2απ(
| ||
| 360 |
| 1 |
| 2 |
| απλ2 |
| 360 |
解答:解:设原来扇形的圆心角为α,半径为λ,
则后来扇形的圆心角为2α,半径为
λ;
由题意得:
=100,
∴
=
×
=50,
∴后来所得的扇形面积是50m2
则后来扇形的圆心角为2α,半径为
| 1 |
| 2 |
由题意得:
| απλ2 |
| 360 |
∴
2απ(
| ||
| 360 |
| 1 |
| 2 |
| απλ2 |
| 360 |
∴后来所得的扇形面积是50m2
点评:该题主要考查了扇形的面积公式及其应用问题;解题的关键是设出圆心角及半径,灵活运用面积公式来分析、解答.

练习册系列答案
相关题目
 如图,圆内接四边形ABCD中,∠A=62°,则∠C=
如图,圆内接四边形ABCD中,∠A=62°,则∠C=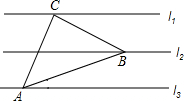 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离均为1,若等腰直角
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离均为1,若等腰直角 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是27cm2,AB=10cm,AC=8cm,则DE的长为
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是27cm2,AB=10cm,AC=8cm,则DE的长为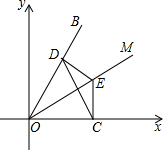 如图,在平面直角坐标系中,在第一象限内,OM与OB是两坐标轴的夹角的三等分线点E是OM上一点,EC⊥X轴于C点,ED⊥OB于D点,OD=8,OE=10
如图,在平面直角坐标系中,在第一象限内,OM与OB是两坐标轴的夹角的三等分线点E是OM上一点,EC⊥X轴于C点,ED⊥OB于D点,OD=8,OE=10