题目内容
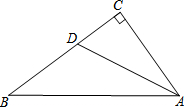如图，∠C=90°，∠BAD=∠CAD，若BC=11cm，BD=7cm，则点D到AB的距离为考点：角平分线的性质
专题：
分析：过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，再根据CD=BC-BD计算即可得解．
解答：
解：如图，过点D作DE⊥AB于E，
∵∠C=90°，∠BAD=∠CAD，
∴DE=CD，
∵CD=BC-BD=11-7=4cm，
∴DE=4cm，
即点D到AB的距离为4cm．
故答案为：4．
解：如图，过点D作DE⊥AB于E，∵∠C=90°，∠BAD=∠CAD，
∴DE=CD，
∵CD=BC-BD=11-7=4cm，
∴DE=4cm，
即点D到AB的距离为4cm．
故答案为：4．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
相关题目
如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是（ ）| A、AB=AC |
| B、BE=CD |
| C、角B=角C |
| D、角ADC=角AEB |
如图，圆内接四边形ABCD中，∠A=62°，则∠C=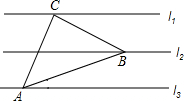
如图，已知l1∥l2∥l3，相邻两条平行直线间的距离均为1，若等腰直角
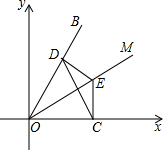如图，在平面直角坐标系中，在第一象限内，OM与OB是两坐标轴的夹角的三等分线点E是OM上一点，EC⊥X轴于C点，ED⊥OB于D点，OD=8，OE=10