题目内容
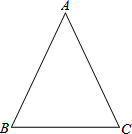 如图,△ABC中,AB=AC=4
如图,△ABC中,AB=AC=4| 5 |
| ||
| 5 |
(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①求证:
 |
| DE |
 |
| CE |
②求点D到BC的距离.
考点:作图—复杂作图
专题:
分析:(1)利用尺规作图作出AC的中点,就是圆心,从而作出圆;
(2)①连接AE,根据等腰三角形的性质证明∠DAE=∠CAE,即可证得;
②连接AE,CD,作DM⊥BC交BC于点M,在直角△BCD中首先利用三角函数求得BD的长,然后在直角△BDH中,利用三角函数求得DM.
(2)①连接AE,根据等腰三角形的性质证明∠DAE=∠CAE,即可证得;
②连接AE,CD,作DM⊥BC交BC于点M,在直角△BCD中首先利用三角函数求得BD的长,然后在直角△BDH中,利用三角函数求得DM.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)①如图,连接AE,
∵AC为直径,
∴∠AEC=90°,
∵AB=AC,
∴∠DAE=∠CAE,
∴
=
;
②连接AE,CD,作DM⊥BC交BC于点M,
∵AC为直径,
∴∠AEC=90°,
∵AB=AC=4
,cosC=
.
∴EC=BE=4,
∴BC=8,
∵AB=AC
∴∠B=∠C
∴cos∠C=cos∠B=
,
∴BD=BC cos∠B=
,
∴DM=BDsin∠B=
.
 解:(1)如图所示:
解:(1)如图所示:(2)①如图,连接AE,
∵AC为直径,
∴∠AEC=90°,
∵AB=AC,
∴∠DAE=∠CAE,
∴
 |
| DE |
 |
| CE |
②连接AE,CD,作DM⊥BC交BC于点M,
∵AC为直径,
∴∠AEC=90°,
∵AB=AC=4
| 5 |
| ||
| 5 |
∴EC=BE=4,
∴BC=8,
∵AB=AC
∴∠B=∠C
∴cos∠C=cos∠B=
| ||
| 5 |
∴BD=BC cos∠B=
8
| ||
| 5 |
∴DM=BDsin∠B=
| 16 |
| 5 |
点评:本题考查了圆周角定理以及三角函数,和等腰三角形的性质,正确理解三角函数的定义是关键.

练习册系列答案
相关题目
 已知△ABC(如图)
已知△ABC(如图) 如图,圆内接四边形ABCD中,∠A=62°,则∠C=
如图,圆内接四边形ABCD中,∠A=62°,则∠C=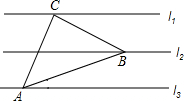 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离均为1,若等腰直角
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离均为1,若等腰直角