题目内容
(1)如图①所示,已知∠AOB=100°,OC是∠AOB平分线,OD、OE分别平分∠COB、∠AOC,求∠DOE的度数;
(2)如图②,在(1)中把“OC是∠AOB的平分线”改为“OC是∠AOB内任意一条射线”,其他任何条件都不变,试求∠DOE的度数;
(3)如图③,在(1)中把“OC是∠AOB的平分线”改为“OC是∠AOB外任意一条射线”,其他任何条件都不变,你能求出∠DOE的度数吗?说明理由.

(2)如图②,在(1)中把“OC是∠AOB的平分线”改为“OC是∠AOB内任意一条射线”,其他任何条件都不变,试求∠DOE的度数;
(3)如图③,在(1)中把“OC是∠AOB的平分线”改为“OC是∠AOB外任意一条射线”,其他任何条件都不变,你能求出∠DOE的度数吗?说明理由.

考点:角平分线的定义,角的计算
专题:探究型
分析:(1)根据角平分线定义求出∠BOC和∠AOC度数,即可得出答案;
(2)根据角平分线定义得出∠COD=
∠BOE,∠COE=
∠AOE,求出∠DOE=∠COD+∠COE=
∠AOB,代入求出即可;
(3)根据角平分线定义得出∠COD=
∠BOE,∠COE=
∠AOE,求出∠DOE=∠COD-∠COE=
∠AOB,代入求出即可.
(2)根据角平分线定义得出∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据角平分线定义得出∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵∠AOB=100°,0C是∠AOB的平分线,
∴∠AOB=∠BOC=
∠AOB=50°,
∵OD、OE分别平分∠BOC、∠AOC,
∴∠COD=
∠BOC=25°,∠COE=
∠AOC=25°,
∴∠DOE=∠COD+∠COE=25°+25°=50°;
(2)∵OD、OE分别平分∠BOC、∠AOC,
∴∠COD=
∠BOE,∠COE=
∠AOE,
∴∠DOE=∠COD+∠COE=
(∠BOE+∠AOE)=
∠AOB=
×100°=50°;
(3)能.
∠DOE=∠DOC-∠COE=
∠BOC-
∠AOC=
(∠BOC-∠AOC)=
∠AOB=
×100°=50°.
∴∠AOB=∠BOC=
| 1 |
| 2 |
∵OD、OE分别平分∠BOC、∠AOC,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COD+∠COE=25°+25°=50°;
(2)∵OD、OE分别平分∠BOC、∠AOC,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COD+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)能.
∠DOE=∠DOC-∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
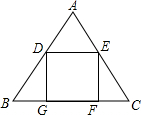 如图,等边三角形ABC中,G、F是BC边上两点,点D、E分别在边AB和AG上,四边形DGFE是长方形,若BG=1,AD=3,则BC=
如图,等边三角形ABC中,G、F是BC边上两点,点D、E分别在边AB和AG上,四边形DGFE是长方形,若BG=1,AD=3,则BC=
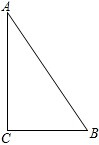 如图所示,△ABC中,AB=1000m,BC=600m,AC=800m,试在△ABC中找一点P,使得P点到A、B、C三点的距离相等,求PC.
如图所示,△ABC中,AB=1000m,BC=600m,AC=800m,试在△ABC中找一点P,使得P点到A、B、C三点的距离相等,求PC.