题目内容
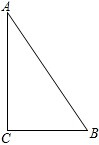 如图所示,△ABC中,AB=1000m,BC=600m,AC=800m,试在△ABC中找一点P,使得P点到A、B、C三点的距离相等,求PC.
如图所示,△ABC中,AB=1000m,BC=600m,AC=800m,试在△ABC中找一点P,使得P点到A、B、C三点的距离相等,求PC.考点:线段垂直平分线的性质,勾股定理的逆定理
专题:
分析:由条件可知△ABC为直角三角形,要使P点到A、B、C三点的距离相等,可知P点为△ABC三边垂直平分线的交点,根据直角三角形的性质可求得P点为AB的中点,可求得PC的长.
解答:解:要使P点到A、B、C三点的距离相等,
可知点P为△ABC三边垂直平分线的交点,
又因为AB=1000m,BC=600m,AC=800m,
所以满足AB2=BC2+AC2,
所以△ABC为直角三角形,
所以点P这AB的中点,
此时PC=PA=PB=
AB=500m.
可知点P为△ABC三边垂直平分线的交点,
又因为AB=1000m,BC=600m,AC=800m,
所以满足AB2=BC2+AC2,
所以△ABC为直角三角形,
所以点P这AB的中点,
此时PC=PA=PB=
| 1 |
| 2 |
点评:本题主要考查垂直平分线的性质及直角三角形的性质、勾股定理的逆定理,掌握直角三角形斜边的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
 如图,已知AB=8,AD=10,AE是折痕.求四边形ABCE的面积.
如图,已知AB=8,AD=10,AE是折痕.求四边形ABCE的面积. 如图所示是由几个小正方块所组成的几何体俯视图,小正方形中的数字表示在该位置小正方块的个数,请你画出这个几何体的正视图和左视图.
如图所示是由几个小正方块所组成的几何体俯视图,小正方形中的数字表示在该位置小正方块的个数,请你画出这个几何体的正视图和左视图.
 根据图中的程序,当输入x=5时,输出的结果y=
根据图中的程序,当输入x=5时,输出的结果y=