题目内容
13．
如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，若∠B=30°，∠BAC=80°，求∠E的度数．
分析 根据三角形的内角和定理求出∠ACD的度数，根据角平分线的定义求出∠ECD的度数，根据三角形外角的性质计算得到答案．
解答 解：∵∠ACD是△ABC的外角，
∴∠ACD=∠B+∠BAC=30°+80°=110°，
∵CE是∠ACD的平分线，∴∠ECD=$\frac{1}{2}$∠ACD=$\frac{1}{2}$×110°=55°，
∵∠ECD是△EBC的外角，
∴∠ECD=∠B+∠E，
∴∠E=∠ECD-∠B=55°-30°=25°．
答：∠E的度数是25°．
点评 本题考查的是三角形外角的性质及三角形的内角和定理，掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3．若y与x成正比，y与z成反比，则下列说法正确的是（ ）
| A． | z是x的正比例函数 | B． | z是x的反比例函数 | ||
| C． | z是x的一次函数 | D． | z不是x的函数 |
要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有OA=OB=OC=OD，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（ ）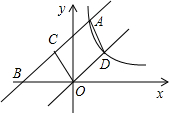
如图，直线y=x+3交反比例函数y=-$\frac{k}{x}$的图象于点A，交x轴于点B，且过点C（-1，2），将直线AB向下平移，线段CA平移到线段OD，当点D也在反比例函数y=-$\frac{k}{x}$的图象上时，则k=-4．
如图：∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°．
如图是小明制作的风筝，为了平衡制成了轴对称图形．已知OC所在的直线是对称轴，∠A=35°，∠BCO=30°，那么∠AOB=130°．