题目内容
7.一直线截△ABC三边AB、AC、BC或其延长线于点D、E、F,求证:$\frac{AD}{BD}•\frac{BF}{CF}•\frac{CE}{AE}=1$.分析 过点B作BG‖CA交EF的延长线于G,根据相似三角形的判定定理得到△BGF∽△CEF,△DBG∽△DAE,于是得到比例式$\frac{BF}{CF}$=$\frac{BG}{CE}$,$\frac{CE}{EA}$=$\frac{CE}{EA}$,$\frac{AD}{DB}=\frac{EA}{BG}$,三式相乘即可得到结论.
解答 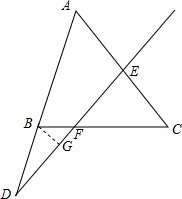 解:过点B作BG‖CA交EF的延长线于G,
解:过点B作BG‖CA交EF的延长线于G,
∴△BGF∽△CEF,△DBG∽△DAE,
∴$\frac{BF}{CF}$=$\frac{BG}{CE}$,$\frac{CE}{EA}$=$\frac{CE}{EA}$,$\frac{AD}{DB}=\frac{EA}{BG}$,
三式相乘得:$\frac{BF}{CF}•\frac{CE}{EA}•\frac{AD}{BD}$=$\frac{BG}{CE}•\frac{CE}{EA}•\frac{EA}{BG}$=1.
点评 本题考查了相似三角形的判定和性质,正确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知A(-2,m)、B(n,$\frac{2}{3}$)是正比例函数y=kx图象上关于原点对称的两点,则k的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
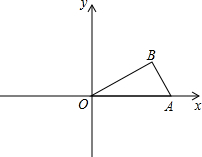 如图,已知放置于平面直角坐标系中的三角板AOB,∠AOB=30°,∠B=90°,AB=1,将△AOB绕O点顺时针旋转30°得到△A1OB1,将△A1OB1绕O点顺时针旋转30°得到△A2OB2,将△A2OB2绕O点顺时针旋转30°得到△A3OB3,依此类推,则B2013的坐标为($\frac{\sqrt{3}}{2}$,-$\frac{3}{2}$).
如图,已知放置于平面直角坐标系中的三角板AOB,∠AOB=30°,∠B=90°,AB=1,将△AOB绕O点顺时针旋转30°得到△A1OB1,将△A1OB1绕O点顺时针旋转30°得到△A2OB2,将△A2OB2绕O点顺时针旋转30°得到△A3OB3,依此类推,则B2013的坐标为($\frac{\sqrt{3}}{2}$,-$\frac{3}{2}$). 如图所示,有一块长方形土地ABCD,分别被甲、乙两人承包,一条公路GEFH穿过这块地,为发展经济,决定将这条公路尽量修直,为不影响甲、乙两家土地面积,请你设计一种方案来解决这个问题.
如图所示,有一块长方形土地ABCD,分别被甲、乙两人承包,一条公路GEFH穿过这块地,为发展经济,决定将这条公路尽量修直,为不影响甲、乙两家土地面积,请你设计一种方案来解决这个问题.