题目内容
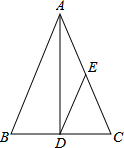 如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长.
如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长.考点:直角三角形斜边上的中线,等腰三角形的性质
专题:
分析:根据等腰三角形的判定得出AB=AC,根据等腰三角形的性质求出∠ADC=90°,根据直角三角形斜边上的中线性质得出DE=
AC,代入求出即可.
| 1 |
| 2 |
解答:解:∵∠B=∠C,
∴AB=AC=8,
∵D为BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵E为AC中点,
∴DE=
AC=4.
∴AB=AC=8,
∵D为BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵E为AC中点,
∴DE=
| 1 |
| 2 |
点评:本题考查了等腰三角形的判定和性质,直角三角形斜边上中线性质的应用,解此题的关键是求出∠ADC=90°和DE=
AC,注意:直角三角形斜边上的中线等于斜边的一半.
| 1 |
| 2 |

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
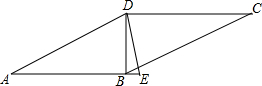 如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.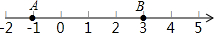 已知数轴上两点A、B对应的数分别为-1、3,数轴上一动点P对应的数为x
已知数轴上两点A、B对应的数分别为-1、3,数轴上一动点P对应的数为x 如图,已知点C是AB的中点,∠A=∠B,AD=BE,MD=NE.求证:△ADC≌△BEC,△MEC≌NDC.
如图,已知点C是AB的中点,∠A=∠B,AD=BE,MD=NE.求证:△ADC≌△BEC,△MEC≌NDC.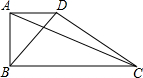 有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.
有一个零件如图所示,要求∠DAB,∠ABC都是直角,工人师傅量得AD=6,AB=8,BC=15,又量得BD=10,AC=17,这个零件符合要求吗,说说你的理由.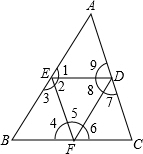 如图,填空:
如图,填空: 如图,
如图,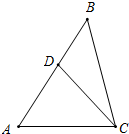 △ABC中,D为AB边上一点,∠B=∠ACD.
△ABC中,D为AB边上一点,∠B=∠ACD.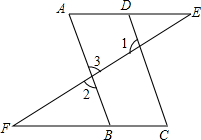 如图,已知∠1+∠2=180°,∠A=∠C,试判断AE与CF的位置关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,试判断AE与CF的位置关系,并说明理由.