题目内容
 如图,已知点C是AB的中点,∠A=∠B,AD=BE,MD=NE.求证:△ADC≌△BEC,△MEC≌NDC.
如图,已知点C是AB的中点,∠A=∠B,AD=BE,MD=NE.求证:△ADC≌△BEC,△MEC≌NDC.考点:全等三角形的判定
专题:证明题
分析:先证出AC=BC,再由已知条件即可证出△ADC≌△BEC;得出CD=CE,再证出CM=CN,即可证出△MEC≌△NDC.
解答:证明:∵点C是AB的中点,
∴AC=BC,
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS);
∴CD=CE,
∴CM=CN,
在△MEC和△NDC中,
∴△MEC≌△NDC(SAS).
∴AC=BC,
在△ADC和△BEC中,
|
∴△ADC≌△BEC(SAS);
∴CD=CE,
∴CM=CN,
在△MEC和△NDC中,
|
∴△MEC≌△NDC(SAS).
点评:本题考查了三角形全等的判定方法SAS;先根据已知条件或求证的结论确定三角形,熟练掌握判定方法SAS是解题的关键.

练习册系列答案
相关题目
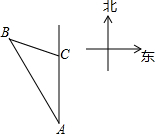 如图,某轮船沿正北方向航行,在点A处测得灯塔B在北偏西30°方向上,轮船以每小时25海里的速度航行2小时到达C后,测得灯塔B在北偏西75°方向上,问轮船到达灯塔B的正东方向时,轮船距灯塔有多远?(结果精确到0.1海里,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.13,
如图,某轮船沿正北方向航行,在点A处测得灯塔B在北偏西30°方向上,轮船以每小时25海里的速度航行2小时到达C后,测得灯塔B在北偏西75°方向上,问轮船到达灯塔B的正东方向时,轮船距灯塔有多远?(结果精确到0.1海里,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.13,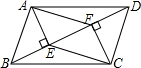 如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:AF=CE.
如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:AF=CE.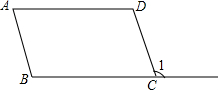 如图,分析图形,完成填空.
如图,分析图形,完成填空. 请你试用a,b,c,d表示如图所示的阴影部分的面积S,并求出当a=3,b=5,c=
请你试用a,b,c,d表示如图所示的阴影部分的面积S,并求出当a=3,b=5,c=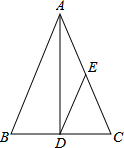 如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长.
如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长. 如图,直线EF分别与直线AB、CD相交于点P和点Q,PG平分∠APQ,QH平分∠CQF,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
如图,直线EF分别与直线AB、CD相交于点P和点Q,PG平分∠APQ,QH平分∠CQF,并且∠1=∠2,说出图中哪些直线平行,并说明理由.