题目内容
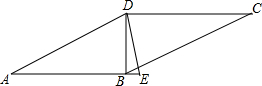 如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.
如图,已知在?ABCD中,对角线BD⊥AB,∠A=30°,DE平分∠ADC交AB的延长线于点E,连接CE.(1)求证:AD=AE;
(2)设AD=12,连接AC交BD于点O,画出图形,并求AC的长.
考点:平行四边形的性质
专题:
分析:(1)根据角平分线的性质可得∠ADE=∠CDE,再根据平行四边形的性质和平行线的性质可得∠CDE=∠AED,利用等量代换可得∠ADE=∠AED,根据等角对等边可得AD=AE;
(2)首先利用勾股定理计算BD=6,再根据勾股定理可得AB长,然后再根据平行四边形的性质可得DN=BN,AN=CN,再利用勾股定理可得AN的值,进而可得答案.
(2)首先利用勾股定理计算BD=6,再根据勾股定理可得AB长,然后再根据平行四边形的性质可得DN=BN,AN=CN,再利用勾股定理可得AN的值,进而可得答案.
解答:(1)证明:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠CDE=∠AED,
∴∠ADE=∠AED,
∴AD=AE;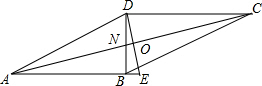
(2)解:∵∠A=30°,AD=12,
∴BD=6,
∴AB=
=6
,
∵四边形ABCD是平行四边形,
∴DN=BN,AN=CN,
∴BN=3,
∴AN=
=3
,
∴AC=6
.
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠CDE=∠AED,
∴∠ADE=∠AED,
∴AD=AE;

(2)解:∵∠A=30°,AD=12,
∴BD=6,
∴AB=
| 122-62 |
| 3 |
∵四边形ABCD是平行四边形,
∴DN=BN,AN=CN,
∴BN=3,
∴AN=
| AB2+BN2 |
| 17 |
∴AC=6
| 17 |
点评:此题主要考查了平行四边形的性质,以及勾股定理的应用,关键是掌握平行四边形对角线互相平分.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图所示,在长为a厘米、宽为
如图所示,在长为a厘米、宽为 如图,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.
如图,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.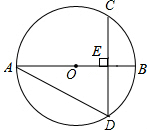 如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2.
如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2. 如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.
如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.
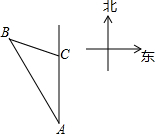 如图,某轮船沿正北方向航行,在点A处测得灯塔B在北偏西30°方向上,轮船以每小时25海里的速度航行2小时到达C后,测得灯塔B在北偏西75°方向上,问轮船到达灯塔B的正东方向时,轮船距灯塔有多远?(结果精确到0.1海里,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.13,
如图,某轮船沿正北方向航行,在点A处测得灯塔B在北偏西30°方向上,轮船以每小时25海里的速度航行2小时到达C后,测得灯塔B在北偏西75°方向上,问轮船到达灯塔B的正东方向时,轮船距灯塔有多远?(结果精确到0.1海里,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.13,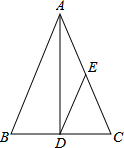 如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长.
如图,在△ABC中,∠B=∠C,D,E分别是BC,AC的中点,AB=8,求DE的长.