Question

14．（1）如图1，已知正方形ABCD，E是AD上一点，F是BC上一点，G是AB上一点，H是CD上一点，线段EF、GH交于点O，∠EOH=∠C，求证：EF=GH；
（2）如图2，若将正方形ABCD改为矩形ABCD，且AD=mAB，其他条件不变，探索线段EF与线段GH的关系并加以证明．

Answer 1

分析 （1）如图1，过点F作FM⊥AD于M，过点G作GN⊥CD于N，EF和GN交于R，GN和MF交于Q，利用正方形的性质得FM=GN=AB=DA，且GN⊥FM，再利用等角的余角相等得到∠OGR=∠OFM，于是可根据“AAS”判定△GNH≌△FME，所以EF=GH；
（2）如图2，过点F作FM⊥AD于M，过点G作GN⊥CD于N，EF、GN交于R，GN、MF交于Q，利用矩形的性质得GN=AD，FM=AB，且GN⊥FM，与（1）一样可得到∠OGR=∠OFM，加上∠GNH=∠FME=90°，则可判断△GNH∽△FME，利用相似三角形的性质得$\frac{GH}{EF}$=$\frac{GN}{FM}$=$\frac{AD}{AB}$，而AD=mAB，所以GH=mEF．

解答 （1）证明：如图1，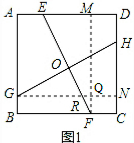
过点F作FM⊥AD于M，过点G作GN⊥CD于N，EF和GN交于R，GN和MF交于Q，
∵四边形ABCD是正方形，
∴FM=GN=AB=DA，且GN⊥FM，
∵∠GOF=∠EOH=∠C=90°，
∴∠OGR=90°-∠GRO=90°-∠QRF=∠OFM，
在△GNH和△FME中
  $\left\{\begin{array}{l}{∠GNH=∠FME}\\{∠HGN=∠EFM}\\{GN=FM}\end{array}\right.$，
∴△GNH≌△FME，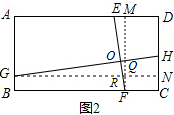
∴EF=GH；
（2）解：GH=mEF．理由如下：
如图2，
过点F作FM⊥AD于M，过点G作GN⊥CD于N，EF、GN交于R，GN、MF交于Q，
∵四边形ABCD是矩形，
∴GN=AD，FM=AB，且GN⊥FM
∵∠GOF=∠EOH=∠C=90°
∴∠OGR=90°-∠GRO=90°-∠QRF=∠OFM，
∵∠GNH=∠FME=90°，
∴△GNH∽△FME，
∴$\frac{GH}{EF}$=$\frac{GN}{FM}$=$\frac{AD}{AB}$=m，
∴GH=mEF．

点评 本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；在运用相似三角形的性质时，主要通过相似比得到线段之间的关系．也考查了全等三角形的判定与性质．