题目内容
4.如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)说明△ADC≌△CEB;
(2)说明AD+BE=DE;
(3)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.

分析 (1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;
(2)由(1)得到AD=CE,CD=BE,即可求出答案;
(3)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,代入已知即可得到答案.
解答 (1)证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中
$\left\{\begin{array}{l}{∠CDA=∠BEC}\\{∠DAC=∠ECB}\\{AC=BC}\end{array}\right.$
∴△ADC≌△CEB(AAS).
(2)证明:由(1)知:△ADC≌△CEB,
∴AD=CE,CD=BE,
∵DC+CE=DE,
∴AD+BE=DE.
(3)DE=AD-BE,
证明:∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ACD=∠CBE}\\{∠ADC=∠BEC}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.
点评 本题主要考查了邻补角的意义,全等三角形的判定和性质等知识点,能根据已知证出符合全等的条件是解此题的关键,题型较好,综合性比较强.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
12.a=5+2$\sqrt{6}$,b=$\frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{3}-\sqrt{2}}}$,则a与b的关系是( )
| A. | a=b | B. | ab=1 | C. | a>b | D. | a<b. |
16.若x1、x2是一元二次方程x2+ax+b=0的两个根,若x1+x2=3,则( )
| A. | a=3 | B. | a=-3 | C. | b=3 | D. | b=-3 |
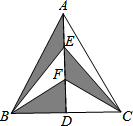 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.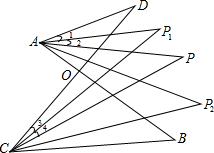 如图中,AP1,AP,AP2是∠DAB的四等分线,CP1,CP,CP2是∠BCD的四等分线,说明∠P与∠P1,P2之间的数量关系.
如图中,AP1,AP,AP2是∠DAB的四等分线,CP1,CP,CP2是∠BCD的四等分线,说明∠P与∠P1,P2之间的数量关系.