题目内容
8．
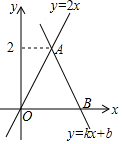如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A，则不等式组$\left\{\begin{array}{l}kx+b＞0\\ kx+b＞2x.\end{array}\right.$的解集为（ ）| A． | x＜1 | B． | x＞2 | C． | 0＜x＜2 | D． | 0＜x＜1 |
分析 先利用正比例函数解析式确定A点坐标，再利用函数图象找出直线y=kx+b在x轴上方且在直线y=2x上方所对应的自变量的范围即可．
解答 解：当y=2时，2x=2，解得x=1，则A（1，2），
当x＜2时，kx+b＞0；
当x＜1时，kx+b＞2x，
所以不等式组$\left\{\begin{array}{l}kx+b＞0\\ kx+b＞2x.\end{array}\right.$的解集为x＜1．
故选A．
点评 本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
相关题目
19．若把分式$\frac{2xy}{x+y}$（x，y为正数）中的x，y分别扩大为原来的2倍，则分式的值是（ ）
| A． | 扩大为原来的2倍 | B． | 缩小为原来的2倍 | C． | 扩大为原来的4倍 | D． | 不变 |
16．
如图，已知AB=AD，∠BAD=∠CAE，则增加以下哪个条件仍不能判断△BAC≌△DAE的是（ ）
如图，已知AB=AD，∠BAD=∠CAE，则增加以下哪个条件仍不能判断△BAC≌△DAE的是（ ）| A． | AC=AE | B． | BC=DE | C． | ∠B=∠D | D． | ∠C=∠E |
如图，将周长为16的三角形ABC沿BC方向平移3个单位得到三角形DEF，则四边形ABFD的周长等于22．
如图，点A（-4，0），B（-1，0），将线段AB平移后得到线段CD，点A的对应点C恰好落在y轴上，且四边形ABDC的面积为9，则D点坐标为（3，3）．