题目内容
3.(1)已知$\sqrt{49}$=x,$\root{3}{y}$=3,z是81的算术平方根,求x-y+z的值.(2)解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$,并写出该不等式组的整数解.
分析 (1)根据平方根、立方根的定义分别得出x、y、z的值,再代入求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解(1)∵$\sqrt{49}$=x,$\root{3}{y}$=3,z是81的算术平方根,
∴x=7,y=27,z=9,
∴x-y+z=7-27+9=-11.
(2)由$\frac{x-3}{2}$+3≥x+1得:x≤1,
由1-3(x-1)<8-x得:x>-2,
所以-2<x≤1,
则不等式组的整数解为-1,0,1.
点评 本题考查的是平方根、立方根及解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
11. 如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
 如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )| A. | x=3 | B. | x=0 | C. | x=-2 | D. | x=-3 |
 如图,在平面直角坐标系xOy中,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴,交直线y=$\frac{1}{2}$x于点B1,以A1为直角顶点,A1B1为直角边,在A1B1的右侧作等腰直角三角形A1B1C1;再过点C1作A2B2∥y轴,分别交直线y=x和y=$\frac{1}{2}$x于A2,B2两点,以A2为直角顶点,A2B2为直角边,在A2B2的右侧作等腰直角三角形A2B2C2…,按此规律进行下去,点C1的横坐标为3,点C2的横坐标为$\frac{9}{2}$,点Cn的横坐标为2×($\frac{3}{2}$)n.(用含n的式子表示,n为正整数)
如图,在平面直角坐标系xOy中,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴,交直线y=$\frac{1}{2}$x于点B1,以A1为直角顶点,A1B1为直角边,在A1B1的右侧作等腰直角三角形A1B1C1;再过点C1作A2B2∥y轴,分别交直线y=x和y=$\frac{1}{2}$x于A2,B2两点,以A2为直角顶点,A2B2为直角边,在A2B2的右侧作等腰直角三角形A2B2C2…,按此规律进行下去,点C1的横坐标为3,点C2的横坐标为$\frac{9}{2}$,点Cn的横坐标为2×($\frac{3}{2}$)n.(用含n的式子表示,n为正整数)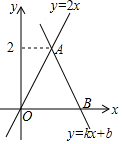 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式组$\left\{\begin{array}{l}kx+b>0\\ kx+b>2x.\end{array}\right.$的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式组$\left\{\begin{array}{l}kx+b>0\\ kx+b>2x.\end{array}\right.$的解集为( ) 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.