题目内容
11.解方程:①3x2=5x+2;
②$\sqrt{2}$x2+4$\sqrt{3}$x=2$\sqrt{2}$
③(y-1)(y+3)+5=0;
④5(x2+1)-7x=0.
分析 ①移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
②移项后求出b2-4ac的值,再代入公式求出即可;
③整理后求出b2-4ac的值,即可得出答案;
④整理后求出b2-4ac的值,即可得出答案.
解答 解:①3x2=5x+2,
3x2-5x-2=0,
(3x+1)(x-2)=0,
3x+1=0,x-2=0,
x1=-$\frac{1}{3}$,x2=2;
②$\sqrt{2}$x2+4$\sqrt{3}$x=2$\sqrt{2}$,
x2+2$\sqrt{6}$x-2=0,
b2-4ac=(2$\sqrt{6}$)2-4×1×(-2)=32,
x=$\frac{-2\sqrt{6}±\sqrt{32}}{2}$
x1=-$\sqrt{6}$+2$\sqrt{2}$,x2=-$\sqrt{6}$-2$\sqrt{2}$;
③(y-1)(y+3)+5=0,
y2+2y+2=0,
b2-4ac=22-4×1×2=-4<0,
所以此方程无解;
④5(x2+1)-7x=0,
5x2-7x+5=0,
b2-4ac=(-7)2-4×5×5=-51<0,
所以此方程无解.
点评 本题考查了解一元二次方程的应用,解此题的关键是能选择适当的方法解一元二次方程,难度适中.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.已知,当x=2时,ax3+bx+7的值是9,当x=-2时,ax3+bx+11的值是( )
| A. | 9 | B. | 5 | C. | -9 | D. | 无法确定 |
1.计算3$\sqrt{2}$-$\sqrt{2}$的值是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
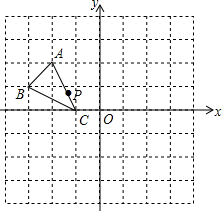 如图,在8×8的方格中建立平面直角坐标系,有点A(-2,2)、B(-3,1)、C(-1,0),P(a,b)是△ABC的AC边上点,将△ABC平移后得到△A1B1C1,点P的对应点为P1(a+4,b+2).
如图,在8×8的方格中建立平面直角坐标系,有点A(-2,2)、B(-3,1)、C(-1,0),P(a,b)是△ABC的AC边上点,将△ABC平移后得到△A1B1C1,点P的对应点为P1(a+4,b+2).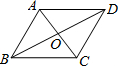 如图,四边形ABCD是平行四边形,AC与BD相交于点O,添加一个条件:AB=BC或AC⊥BD等,可使它成为菱形.
如图,四边形ABCD是平行四边形,AC与BD相交于点O,添加一个条件:AB=BC或AC⊥BD等,可使它成为菱形.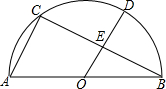 如图,已知点C,D是半圆$\widehat{AB}$上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:
如图,已知点C,D是半圆$\widehat{AB}$上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论: