题目内容
8.∠AOB=90°,∠COD=60°,OE平分∠AOC,OF平分∠BOD.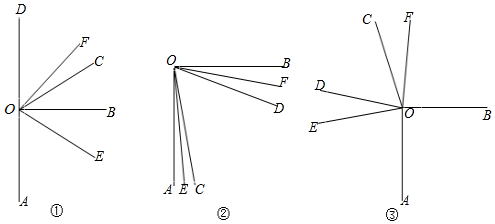
(1)如图1,当A,O,D三点共线时,则∠EOF=75°
(2)将∠COD绕点O顺时针方向旋转至如图2所示位置,∠COD的两边OC,OD都在∠AOB的内部,求∠EOF的度数;
(3)当∠COD旋转至如图3所示位置,作∠EOF的角平分线ON,求∠EON的度数.
分析 (1)根据平角的定义可求∠AOC,∠BOD的度数,再根据角平分线的定义求得∠AOE,∠FOD的度数,再根据平角的定义可求∠EOF的度数;
(2)设∠AOE=∠COE=x,根据角的和差关系得到∠BOD=30°-2x,根据角平分线的定义得到∠BOF=15°-x,再∠EOF=∠AOB-(∠AOE+∠BOF)即可求解;
(3)设∠BOC=2x,则∠AOC=360°-∠AOB-∠BOC=270°-2x,∠BOD=∠BOC+∠COD=2x+60°,根据角平分线的定义得到∠COE=$\frac{1}{2}$∠AOC=135°-x,同理∠DOF=$\frac{1}{2}$∠BOD=x+30°,可得∠EOF=∠COE+∠DOF-∠COD=105°,再根据角平分线的定义得到∠EON的度数.
解答 解:(1)∵∠COD=60°,∠AOB=90°,
∴∠AOC=120°,∠BOD=90°,
∵OE平分∠AOC,OF平分∠BOD,
∴∠AOE=60°,∠FOD=45°,
∴∠EOF=180°-60°-45°=75°;
(2)∵OE平分∠AOC,
∴设∠AOE=∠COE=x,
∴∠BOD=∠AOB-∠AOC-∠COD=90°-2x-60°=30°-2x,
又∵OF平分∠BOD,
∴∠BOF=$\frac{1}{2}$∠BOD=$\frac{1}{2}$(30°-2x)=15°-x,
∴∠EOF=∠AOB-(∠AOE+∠BOF)=90°-(x+15°-x)=75°,
(3)设∠BOC=2x,
则∠AOC=360°-∠AOB-∠BOC=360°-90°-2x=270°-2x,
∠BOD=∠BOC+∠COD=2x+60°,
∵OE平分∠AOC,
∴∠COE=$\frac{1}{2}$∠AOC=135°-x,
同理∠DOF=$\frac{1}{2}$∠BOD=x+30°,
∴∠EOF=∠COE+∠DOF-∠COD=105°,
又∵ON平分∠EOF
∴∠EON=$\frac{1}{2}$∠EOF=52.5°.
故答案为:75°.
点评 本题考查的是角的计算,角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案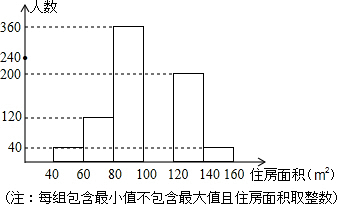 某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:
某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 200 | 300 | 400 | 70 | 30 |
(1)根据表格可得,被调查的消费者平均年收入为2.63万元;被调查的消费者年收入的中位数是2.4万元;众数是3.0万元.
(2)补全分布直方图;
(3)根据频数分布直方图,求打算购买100-120平方米住房的人数及打算购买住房面积小于100平方米的消费者人数占被调查消费者人数的百分数.
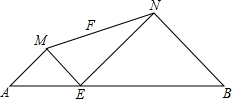 如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.
如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.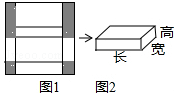 图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.
图1是边长为30的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知长方体的宽是高的2倍,求该长方体盒子的体积和表面积.