题目内容
 如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.考点:解直角三角形的应用-仰角俯角问题,矩形的性质
专题:几何图形问题,数形结合
分析:首先过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,易得四边形ABFE为矩形,根据矩形的性质,可得AB=EF,AE=BF.由题意可知:AE=BF=1100-200=900米,CD=1.99×104米,然后分别在Rt△AEC与Rt△BFD中,利用三角函数即可求得CE与DF的长,继而求得两海岛间的距离AB.
解答: 解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=1100-200=900米,CD=1.99×104米=19900米.
在Rt△AEC中,∠C=45°,AE=900米.
∴CE=
=
=900(米).
在Rt△BFD中,∠BDF=60°,BF=900米.
∴DF=
=
=300
(米).
∴AB=EF=CD+DF-CE=19900+300
-900=19000+300
(米).
答:两海岛间的距离AB为(19000+300
)米.
 解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=1100-200=900米,CD=1.99×104米=19900米.
在Rt△AEC中,∠C=45°,AE=900米.
∴CE=
| AE |
| tan45° |
| 900 |
| 1 |
在Rt△BFD中,∠BDF=60°,BF=900米.
∴DF=
| BF |
| tan60° |
| 900 | ||
|
| 3 |
∴AB=EF=CD+DF-CE=19900+300
| 3 |
| 3 |
答:两海岛间的距离AB为(19000+300
| 3 |
点评:此题考查了俯角的定义、解直角三角形与矩形的性质.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,三角板的直角顶点P在射线OM上,∠AOB=90°,OM是∠AOB的角平分线
如图,三角板的直角顶点P在射线OM上,∠AOB=90°,OM是∠AOB的角平分线 已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF.
已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF. 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.
如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.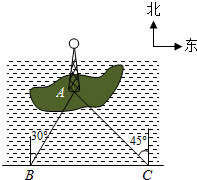 如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.
如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.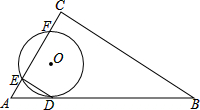 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.